What is Dimension in Physics
The dimension of a physical quantity shows the application of the method of fundamental quantities like Mass (M), Length (L), and Time (T) to relate the fundamental units of a physical quantity. In dimension, we derive quantities by applying physical quantities. To understand dimension, we need to understand the method of measurements, fundamental quantities, derived quantities, and even their corresponding units in physics.
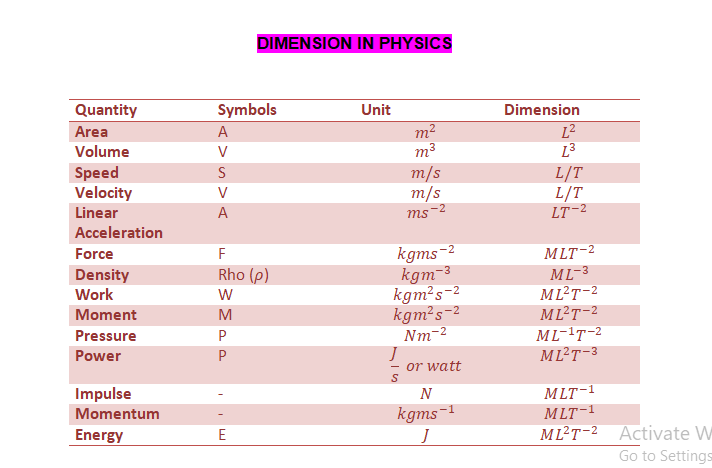
This dimension helps us in finding the relationship between quantities. As we mentioned earlier, we apply Mass in the form of M, Length in the form of L, and Time in the form of T. Additionally, units like temperature will be in the form of K or θ, electric current in the form of (A) which is an expression for ampere, and finally luminous intensity as (II). Below are 2 videos explaining dimensions and their calculations.
Video 1
Video 2
The Fundamental Dimensions
Physics identifies several base quantities, each with its own dimension:
• Length (L): Measures distance.
• Mass (M): Quantifies the amount of matter.
• Time (T): Tracks the progression of events.
• Electric Current (I): Represents the flow of electric charge.
• Thermodynamic Temperature (Θ): Indicates the thermal state.
• Amount of Substance (N): Counts entities like atoms or molecules.
• Luminous Intensity (J): Measures the perceived power of light.
These foundational dimensions serve as building blocks for all other physical quantities.
Derived Dimensions and Their Significance
By combining base dimensions, we derive dimensions for other physical quantities. For example:
• Velocity: Expressed as length per unit time (L/T), indicating how position changes over time.
• Force: Defined as mass times acceleration (ML/T²), representing the interaction that changes an object’s motion.
• Energy: Calculated as force applied over a distance (ML²/T²), denoting the capacity to perform work.
Table of Dimensions in Physics
| QUANTITY | DIMENSION |
| Speed | LT-1 |
| Velocity | LT-1 |
| Acceleration | LT-2 |
| Force | MLT-2 |
| Tensile stress | ML-1T-2 |
| Elastic Force | MLT-2 |
| Young Modulus | ML-1T-2 |
| Work done in elastic spring/string | ML2T-2 |
| Work | ML2T-2 |
| Work done horizontal | ML2T-2 |
| Work done vertical | ML2T-2 |
| Kinetic energy | ML2T-2 |
| Potential energy | ML2T-2 |
| Power | ML2T-3 |
| Projectile time of flight | T |
| Projectile maximum height | L |
| Projectile range | L |
| Moment of force | ML2T-2 |
| Density | ML-3 |
| Upthrust | MLT-2 |
| Centripetal acceleration | LT-2 |
| Centripetal force | MLT-2 |
| Linear velocity | LT-1 |
| Linear acceleration | LT-2 |
| Period | T |
| Frequency | T-1 |
| Period of simple pendulum | T |
| Momentum | MLT-1 |
| Impulse | |
| Pressure | ML-1T-2 |
| Work done by expanding gas | ML2T-2 |
| Wavelength | M |
| Wave velocity | LT-1 |
| Gravitational Force | MLT-2 |
| Gravitational potential | L2T-2 |
| Escape velocity | LT-1 |
| Electric force | MLT-2 |
| Magnetic force | MLT-2 |
You may also like to read:
SS1 Lesson Note: Introduction to Physics For First Term
How to Calculate Dimensions of Physical Quantity
To calculate the dimensions of a physical quantity, we need to be guided on the measurement of quantities in units of Length, Mass, and Time. These involve the dimensions Length (L), Mass (M), and Time (T) respectively. To find the dimension of any quantity, we substitute the units of the quantity into L, M, and T. You insert the symbols into a bracket in this way: [L], [M], and [T]. For example, to find the dimension of speed, we first write the formula as
Speed = Distance / Time
We know that the unit for Distance = meter (m) and meter is a length, which can be, Dimension of Distance = [L]
Note: We only have m which is [L]. If we have m2, we can now write [L2], and Time is in seconds which can also be T, Thus, the dimension of Time = T, To derive the dimension of speed, we say: Speed = Distance / Time. This implies that Speed = [L] / [T]. Therefore, the dimension of Speed = [LT-1] or [L][T-1].
Worked Examples on Dimension in Physics
Here are examples to make you understand dimension in physics: how to calculate dimensions of physical quantities
Example 1
- Find the dimension of an Area and Volume.
Solution:
For Area = Length x Breadth
Which shows that the dimension of Area = [L] x [L] = [L2]
Now, since volume = Length x Base x Height
The dimension of volume = [L] x [L] x [L] = [L3]
Example 2
2. Deduce the dimension of (a) force and (b) Pressure
Solution:
(a) force = mass x acceleration
which shows that
Dimension of force = dimension of mass x dimension of acceleration
and the Dimension of mass = [M]
while the Dimension of acceleration = Dimension of Velocity / Dimension of Time
and Dimension of Velocity = Dimension of Displacement [L] / Dimension of Time [T]
Thus, Dimension of Velocity = [L] / [T] = [L] [T-1] or [LT-1]
Therefore, by substituting the dimensions of velocity and time into acceleration,
we have
dimension of acceleration = [LT-1] / [T] = [LT-2]
Now, to finally derive the acceleration of force,
we say
Dimension of force = [M] x [LT-2] = [M] [LT-2] or [MLT-2]
(b) To find the dimension of pressure
We apply the formula pressure = force / area
which means Dimension of pressure = Dimension of force / Dimension of area
and Dimension of force = Dimension mass x Dimension of acceleration
you can remember that we earlier calculated the dimension of force as [MLT-2]
Also, Dimension of area = [L] x [L] = [L2]
Thus, Dimension of pressure = [MLT-2] / [L2]
This implies
Dimension of pressure = [ML-1T-2]
Example 3
Find the dimension of the following:
a. work
b. Velocity
c. Linear acceleration
d. Power
e. Pressure
f. Momentum
g. Impulse
Solution:
a. Work = Force x Distance
Dimension of Work = Dimension of Force x Dimension of Distance
Therefore, Dimension of Work = MLT-2 x L
This implies that, Dimension of work = ML2 T-2
b. Velocity = Displacement / Time = L / T = LT-1
c. Acceleration = Velocity / Time = LT-1 / T = LT-2
d. Power = work done / time = ML2 T-2 / T = ML2 T-3
e. Pressure = Force / Area = MLT-2 / L3 = ML-2T-2
f. Momentum = mass x velocity = M x LT-1 = MLT-1
g. Impulse = Force x Time = MLT-2 x T = MLT-1
Example 4
Find the dimension in the electrical system of the following:
a. Electric charge
b. Electrical Potential (voltage)
c. Capacitance (c)
Solution:
a. To find electric charge, we use the formula
electric charge = current (A) x time (T)
Thus, electric charge = [A] x [T] = [AT]
b. Electric potential (voltage) = power / current
Dimension voltage = ML2 T-3 / A = [MA-1L2 T-3]
c. Capacitance = charge / potential = [AT] / [MA-1L2 T-3]
Thus, capacitance = [M-1A2L-2 T4]
The Role of Dimensional Analysis
Dimensional analysis is a powerful tool in physics, allowing us to:
• Verify Equations: Ensuring both sides of a physical equation have the same dimensions confirms its validity.
• Derive Relationships: By analyzing the dimensions involved, we can deduce how different quantities depend on each other.
• Convert Units: Facilitates transitioning between measurement systems by understanding the underlying dimensions.
Beyond the Observable: Higher Dimensions
While our everyday experience is confined to three spatial dimensions and one temporal dimension, theoretical physics ventures into higher-dimensional spaces:
• Fourth Dimension: Incorporates time with the three spatial dimensions, forming the fabric of spacetime in Einstein’s theory of relativity.
• Fifth Dimension and Beyond: Theories like Kaluza-Klein propose additional dimensions to unify fundamental forces, suggesting that these extra dimensions are compactified or “curled up” at scales beyond current detection.
These higher dimensions, though not directly observable, provide profound insights into the fundamental nature of the universe.
Dimensions in Mathematics and Beyond
In mathematics, dimensions extend beyond physical interpretation:
• Fractal Dimensions: Describe complex, self-similar structures that don’t conform to traditional integer dimensions, offering insights into patterns found in nature.
• Abstract Spaces: Concepts like phase space in physics utilize higher-dimensional mathematical spaces to represent all possible states of a system.
These mathematical frameworks enrich our understanding and modeling of complex systems.
Reference