Velocity Definition: What is Velocity in Physics?
Velocity Definition: Velocity refers to the rate of change of an object’s position with respect to time, in a particular direction. Similarly, we can define velocity in simple terms as the rate of change of displacement in a specific direction. Therefore, velocity is a vector quantity and it takes into account both the object’s speed and direction of motion. The SI unit of the velocity of an object is in meters per second (m/s) or any other unit of length per unit of time.

Velocity Formula in Physics
The Velocity formula is:
Velocity = Displacement / Time
The symbol for velocity is v, displacement is s, and time is t.
Hence, we can rewrite the formula for velocity as v = x / t.
Where
Displacement (x) is the change in an object’s position in a sepcific direction, and
Time (t) is the duration over which the change occurs
Units of Velocity in Physics
According to our definition, velocity is a measure of how fast a body moves in a particular or specific direction by taking time into consideration.
Therefore, if we apply the formula, we will see that
Velocity = displacement x (measured in meters according to the si units) / time t (measured in seconds)
v = x / t
Thus, when we substitute the formula with their respective units, we will have
v = x / t = m / s = meter per second
Therefore, we can finally see how we arrived at the si unit of velocity (m/s) which is currently in use all over the world as at the time of updating this article (2 Aug 2023). Meters per second is a derived unit of length and time
Hence, the units of velocity are commonly expressed as meters per second (m/s) in the International System of Units (SI).
Meters (m) represent the unit of displacement, and seconds (s) represent the unit of time. When we say an object is moving at a velocity of 5 m/s, it means that it covers 5 meters of distance (in a specific direction) in one second in a particular direction.
To calculate velocity, you divide the change in an object’s position (distance travelled) by the time taken to cover that distance. So, if an object travels 50 meters in 10 seconds, its velocity would be 50 meters divided by 10 seconds, which equals 5 m/s.
Additionally, we can measure velocity in meters per second (m/s), kilometres per hour (km/h), feet per second (ft/s), or miles per hour (mph). The choice of the unit depends on the application and the preference of the user. But the most common and acceptable unit is m/s.
Velocity Definition – Explanation
Velocity is a fundamental concept in physics that describes the rate of change of a distance in a specific direction with respect to time.
It is a vector quantity that includes both the speed and direction of motion. Velocity definition is important for understanding the behaviour of moving objects and is essential in many areas including mechanics, astrophysics, and engineering.
Additionally, velocity definition is the measurement of the displacement of an object per unit of time, in a particular direction. It is a fundamental concept in physics, and its understanding would help in many fields.
Furthermore, velocity is very important in classical mechanics, this is because it describes the motion of objects under the influence of external forces, such as gravity or friction.
Therefore, as we go deeper into this article, it will help us to understand what is velocity, the different kinds of velocity, its importance, and its applications in various fields. We will also discuss the difference between velocity and speed, the formula for calculating velocity, and the units of measurement used.
Indeed, this comprehensive article encompasses everything you need to know about velocity in Physics. Here we go!
What is Initial Velocity?
Initial velocity, in simple terms, refers to the speed and direction of an object at the very beginning of its motion or a particular event. It helps us to understand the motion of objects in Physics.
Imagine you throw a ball horizontally or vertically into the air. At the exact moment, you release the ball, it possesses a certain velocity, either upwards, downwards, or sideways, depending on how you throw it. This velocity at the initial moment is called the initial velocity.
The initial velocity is important because it sets the foundation for how the object’s motion will evolve over time. As the object moves, other forces like gravity, air resistance, or friction may act on it, affecting its velocity.
By knowing the initial velocity and understanding the forces at play, we can predict the object’s future motion using physics equations.
In equations of motion, the initial velocity is often represented as “fi” or “u” or “v₀”. It allows scientists, engineers, and anyone studying motion to analyze and calculate various aspects, such as the distance travelled, time taken, or final velocity reached by the object during its journey.
If we are to define the change in velocity (ΔV) as the initial velocity (u) subtracted from final velocity (v). Therefore we can write the formula for change in velocity in mathematical form as: ΔV = v – u
Hence, we can conclude that the initial velocity formula is u = v + ΔV
What Does Vo Mean in Physics?
To perfectly understand what does vo mean in physics? We need to have a knowledge of initial velocity. From our previous explanation, we have seen that the initial velocity can be represented by using any of the symbols “v₀”, “fi” or “u”.
Therefore, in simple terms, v₀ means original velocity, initial velocity, or velocity from origin. You may come across v₀ as you continue your journey into the fountain of physics, engineering, science fields and even mathematics.
Hence, you need to understand that v₀ is a symbol assigned by your Teacher, the publisher of the book you are reading in order to denote initial velocity.
What is Final Velocity?
Final velocity (v), in simple terms, refers to the speed and direction of an object at the end of its motion or a particular event. It is a key concept in physics. It helps us to understand how an object’s speed changes during its journey.
When you throw a ball into the air or push a car forward, it accelerates or decelerates due to various forces acting upon it.
At the exact moment when the ball reaches its highest point or the car comes to a stop, it has a specific velocity. This velocity at the end of the motion or event is called the final velocity.
Understanding the final velocity is important because it helps us assess how fast an object is moving at the conclusion of its motion and in which direction it is heading.
This information is useful for safety purposes, designing vehicles, predicting impact forces, and other practical applications.
In physics equations, the symbol for final velocity is “v” or “vₓ,” depending on the context. By comparing the initial velocity (if known) with the final velocity, we can calculate changes in speed and direction, which enable us to better comprehend the behaviour of moving objects.
Similarly, we can use the ΔV = v – u to find the final velocity. Which implies that
v = u + ΔV
Change in Velocity
Change in velocity refers to the difference between an object’s final velocity and its initial velocity during a specific time interval.
It is a measure of how much the object’s speed and direction have altered over that period. The formula for change in velocity (Δv) is simply the final velocity (v) minus the initial velocity (u).
Mathematically, we can say that the change in velocity formula is: Δv = v – u.
Positive Δv indicates an increase in speed or a change in direction, while negative Δv suggests a decrease in speed or a change in the opposite direction.
How to Calculate Velocity
Calculating velocity depends on the question available to you due to different equations of velocity. Therefore, to Calculate velocity in physics involves determining the speed and direction of an object’s motion.
Thus, we can follow these three simple steps to calculate velocity:
Step 1: Measure Initial and Final Positions:
Choose a specific time interval during which you want to calculate velocity. Measure the initial position (xi) of the object at the beginning of the interval and the final position (xf) at the end of the interval. Make sure to use the same units of measurement for both positions, such as meters.
Step 2: Find the Change in Position:
Calculate the change in position (Δx) by subtracting the initial position from the final position: Δx = xf – xi. This value represents the distance in a specific direction (displacement) the object has moved during the time interval.
Step 3: Determine the Time Taken:
Measure or know the time (t) it took for the object to move from the initial to the final position. Make sure to use consistent units of time, such as seconds.
Step 4: Calculate Velocity:
Now that you have the change in position (Δx) and the time taken (t), you can calculate the velocity (v) using the formula: v = Δx / t. This formula gives you the average velocity of the object during the chosen time interval. If the motion was in one dimension (e.g., straight line), this velocity would have both magnitude (speed) and direction, making it a vector quantity.
In summary, to calculate velocity, measure the initial and final positions, find the change in position, determine the time taken, and use the formula v = Δx / t to calculate the average velocity of the object. Where Δx = displacement.
Velocity Solved Problem
A car travels at an average velocity of 100 km/h. What distance does it cover in 5 minutes?
Solution
100 km/h = (100/60) km/minute
Velocity = Displacement/time
Displacement = velocity x time = (100/60) x 5 = 8.3 km
Average Velocity
Average velocity is the average speed and direction of an object over a certain time interval. It is calculated by dividing the change in the object’s position (displacement) during that time by the time taken.
Average velocity = Total Displacement / Time taken
or
Average velocity = Change in displacement / Time
For example, if an object moves 20 meters east in 5 seconds, its average velocity would be 4 meters per second east. Average velocity gives an overall picture of how fast and in which direction the object moves during the specified time, even if its speed changes throughout.
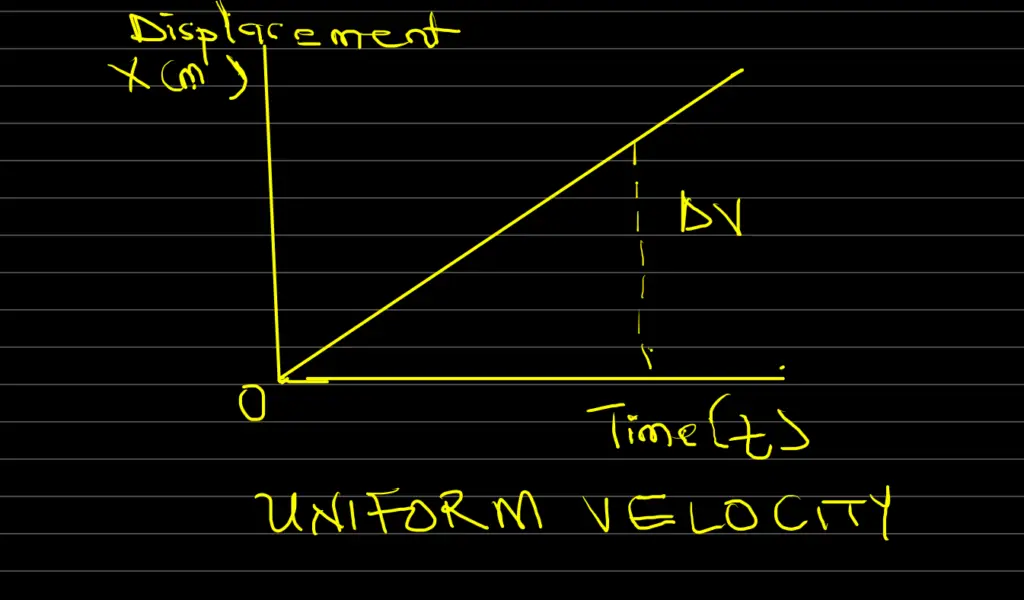
Uniform and Non-Uniform Velocity
Uniform velocity and non-uniform velocity are terms used to describe how the speed of an object changes during its motion.
Additionally, uniform velocity means that the object moves in a straight line and covers an equal amount of distance in an equal amount of time. In other words, its speed remains constant.
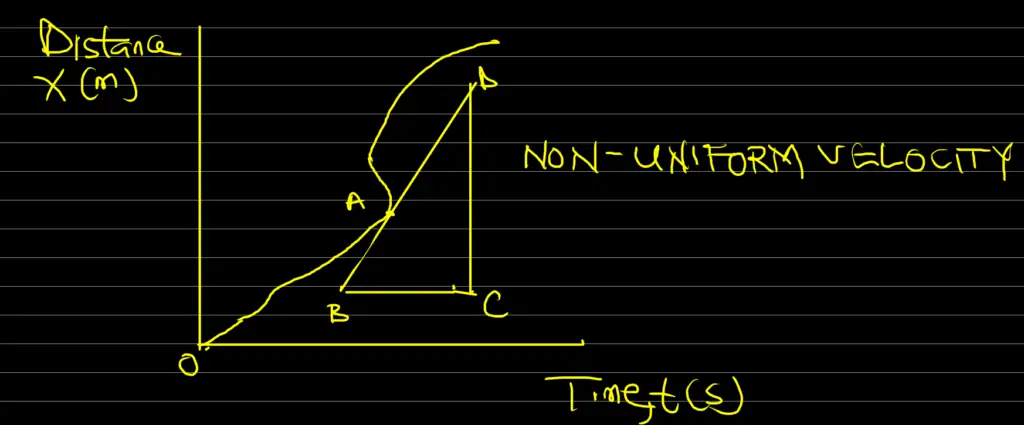
Non-uniform velocity, on the other hand, means that the object’s speed changes over time. It can either speed up, slow down or change direction during its motion.
Instantaneous Velocity
Instantaneous velocity refers to the speed and direction of an object at an exact moment in time. Unlike average velocity, which considers the overall motion during a time interval, instantaneous velocity focuses on a specific instant.
To determine instantaneous velocity, you must find the object’s velocity at that precise moment, which can be done by taking the limit of the change in position over an infinitesimally small time interval.
This concept helps us in understanding an object’s behaviour at any given point during its motion, especially when its speed or direction is changing continuously.
Displacement-Time Graph
A displacement-time graph, also known as a position-time graph, is a visual representation that shows how an object’s position (displacement) changes over a specific period.
On the graph, time is plotted on the x-axis (horizontal) and displacement on the y-axis (vertical). The slope of the graph at any point represents the object’s instantaneous velocity at that moment. A steeper slope indicates higher velocity. If the graph is a straight line, it suggests uniform velocity.
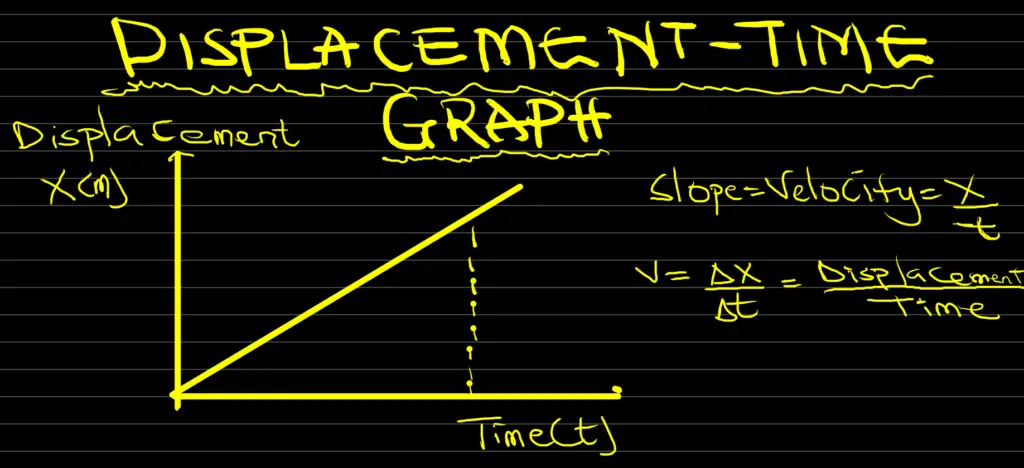
Curved lines indicate non-uniform motion, with changing velocity. Displacement-time graphs are essential for understanding an object’s journey and its speed variations.
Velocity-Time Graph
A velocity-time graph also called a speed-time graph, illustrates how an object’s velocity changes over a specific time period. On the graph, time is plotted on the x-axis (horizontal) and velocity on the y-axis (vertical).
The slope of the graph at any point represents the object’s acceleration at that moment. A steeper slope indicates higher acceleration. A flat line represents constant velocity (uniform motion), while a curve indicates changing velocity (non-uniform motion).
Velocity-time graphs are useful in understanding how an object’s speed changes over time and provide valuable information about its acceleration and deceleration during its journey.
Velocity Equations
Velocity is the measure of an object’s speed and direction. There are two important equations to calculate velocity:
- Average Velocity (vavg): It is found by dividing the change in position (displacement, Δx) by the time taken (Δt). The formula is vavg = Δx / Δt.
- Instantaneous Velocity (vinstantaneous): It represents an object’s velocity at a specific instant. To find it, you take the derivative of the object’s position-time equation with respect to time. In calculus notation: vinstantaneous = d(x) / dt.
We also have equations of motion where velocity is involved:
v = u + at
v2 = u2 + 2as
Therefore, both equations provide valuable insights into an object’s motion, whether it’s moving at a constant speed or changing its velocity over time.
Velocity Dimension
Velocity is a physical quantity with dimension [L/T], which stands for length per time (e.g., meters per second). To derive this dimension, we consider that velocity is the rate of change of position (length) over time.
Therefore, Velocity = Displacement / Time = Meters / Second
Since the unit of displacement is in meters (which is length, L), while the si unit of time is in seconds (T). We can conveniently say that:
Velocity = Length (L) / Time (T) = L / T
This is taking into account that the symbol of Length in dimension is in L, while the symbol for time in dimension is in T.
As you can see, we have obtained the dimension of velocity by Dividing length (L) by time (T) which gives us the dimension [L/T] or [LT-1].
By analyzing how velocity is calculated (change in position divided by the time taken), we can see that the units match the [L/T] dimension.
Velocity vs Speed: What is the Difference?
We use both speed and velocity to describe how fast an object is moving. However, there is a significant difference between the two. While velocity takes into account both the speed and direction of motion, speed only considers the magnitude of motion.
For example, if a car travels 100 meters in 10 seconds, the speed of the car is 10 m/s. However, if the car travels 100 meters in 10 seconds, but changes direction and returns to its original position, its velocity is zero, as its displacement is zero.
When we talk about speed, we are looking at how fast a body moves but not in a specific direction. Therefore, we consider speed as a scalar quantity. Additionally, we define speed as the ratio of distance to time. Thus, we can write the formula for speed as (speed=distance/time) s=d/t. They both have the same unit which is meters per second (m/s).
On the other hand, velocity is due to how fast an object is moving in a specific direction. For velocity, we consider displacement and time. Therefore, this signifies that velocity is a vector quantity because of the presence of displacement instead of distance.
Table of Velocity vs Speed
Here is a table comparing velocity and speed:
| Velocity | Speed |
|---|---|
| Considers both magnitude and direction | Considers only magnitude |
| Vector quantity | Scalar quantity |
| Example: 10 m/s east | Example: 10 m/s |
| Can be positive or negative | Always positive or zero |
| Measured in units like m/s or km/h | Measured in units like m/s or km/h |
In this table, we can see the key differences between velocity and speed. Remember, velocity considers both the magnitude and direction of motion, making it a vector quantity.
However, speed only takes into account the magnitude, making it a scalar quantity. Velocity can be positive or negative depending on the direction of motion, whereas speed is always positive or zero.
Both are measured in units like meters per second (m/s) or kilometres per hour (km/h).
What is Speed?
We can define speed as the rate of change of distance with time. Additionally, we need to understand that speed is a measure of how fast an object moves, without considering its direction. The si unit of speed is in meters per second. The formula for calculating speed is
Speed = Distance / Time
Speed is a scalar quantity, meaning it has magnitude but no specific direction. For example, if a car travels at 50 kilometres per hour, its speed is 50 km/h.
Velocity Constant
In physics, a velocity constant refers to a situation where an object’s velocity remains constant over time. When an object moves with constant velocity, it means its speed and direction do not change.
This occurs when there is a balance of forces acting on the object, resulting in no acceleration. For instance, if you roll a ball on a smooth, flat surface with no external forces, it will maintain a constant velocity.
In such cases, the velocity constant simplifies calculations, as there is no need to account for changing speed or direction during the object’s motion.
Examples of Velocity
Here are ten examples of velocity:
- Car driving at 60 kilometres per hour eastwards.
- Bird flying at 15 meters per second northwards.
- A rocket ascends at 500 meters per second vertically.
- A person running at 8 feet per second in a southwest direction.
- A boat moving at 25 knots southeastwards.
- An athlete sprints at 10 meters per second towards the finish line.
- A bicycle moving at 20 kilometres per hour westwards.
- A tennis ball launched at 30 meters per second upwards.
- A train travelling at 100 miles per hour northbound.
- A satellite orbiting Earth at 7 kilometres per second in a circular path.
Velocity Applications: Where is Velocity Used?
Velocity is a fundamental concept in physics and has many practical applications. Its applications range from calculating the motion of planets and stars to designing high-speed vehicles, such as aeroplanes and rockets.
Some of the areas where we can use velocity include:
1. Mechanics
In mechanics, we use velocity to describe the motion of objects under the influence of external forces. Thus, we use it to calculate the acceleration of objects and determine the time taken to reach a particular position.
2. Astrophysics
In astrophysics, velocity helps us to study the motion of planets, stars, and galaxies. We use it to calculate the velocity of celestial bodies and determine their mass, distance, and composition.
3. Engineering
In engineering, velocity is used to design high-speed vehicles, such as airplanes and rockets. Thus, we can calculate the aerodynamic drag and lift of objects. Additionally, we can determine the maximum speed and altitude that they can achieve.
Frequently Asked Questions
- What is Velocity in simple terms?
Velocity is the rate of change of an object’s position with respect to time, in a particular direction. It is a vector quantity that takes into account both the object’s speed and direction of motion.
- How is Velocity different from Acceleration?
Acceleration is the rate of change of an object’s velocity with respect to time. It is a vector quantity that takes into account both the object’s speed and direction of motion. Velocity, on the other hand, is the rate of change of an object’s position with respect to time, in a particular direction.
- What is the formula for calculating Velocity?
The Velocity formula is given by Velocity = Displacement / Time. Where Displacement is the change in an object’s position, and time is the duration over which the change occurs.
- What are the units of Velocity?
The unit of velocity is measured in length per unit of time. The s.i unit of velocity is in meters per second (m/s), kilometers per hour (km/h), feet per second (ft/s), or miles per hour (mph).
- What is the difference between Velocity and Speed?
Velocity takes into account both the speed and direction of motion, while speed only considers the magnitude of motion.
- What are some applications of Velocity?
Velocity has many practical applications, ranging from calculating the motion of planets and stars to designing high-speed vehicles, such as airplanes and rockets.
Conclusion
Velocity is a fundamental concept in physics that describes the rate of change of an object’s position with respect to time, in a particular direction. It is a vector quantity that includes both the speed and direction of motion.
In this article, we have discussed the Velocity definition, its importance, and its applications in various fields. We have also explored the difference between velocity and speed, the formula for calculating velocity, and the units of measurement used.
You may also like to read: