What is Centripetal Acceleration?
Definition: Centripetal acceleration is the type of acceleration that is directed toward the center of a circular path. The centripetal acceleration si unit is in meters per second square (ms-2), and its symbol is a.
The formula for centripetal acceleration is a = v2/r or a = ω2r
[where a = centripetal acceleration, v = speed, ω = angular velocity, and r = radius of the circular path]
When you enter a merry-go-round, it will go around a circular path about an axis. its continuous movement would make you feel like you are being pushed outside. You are experiencing this outward push because the merry-go-round keeps changing direction in a circular path while your body wants to continue moving in a straight line.
Therefore, as the object keeps rotating, centripetal force provides sufficient force to help your body continue moving around the circular path. Additionally, centripetal acceleration is directed toward the center of the circular path.
Many people kept asking a question as to whether centripetal acceleration is constant. The answer is Yes, and this is because the speed of the object is constant in magnitude but its direction is changing along a circular path. Thus, it is important to know that this type of acceleration is experienced by any object undergoing circular motion. It’s always directed toward the center.
Centripetal Acceleration Derivation
The acceleration of an object moving in a circle:
- Is always directed toward the center of the circle.
- It has a constant magnitude
Therefore, we can derive the mathematical equation using the diagram below
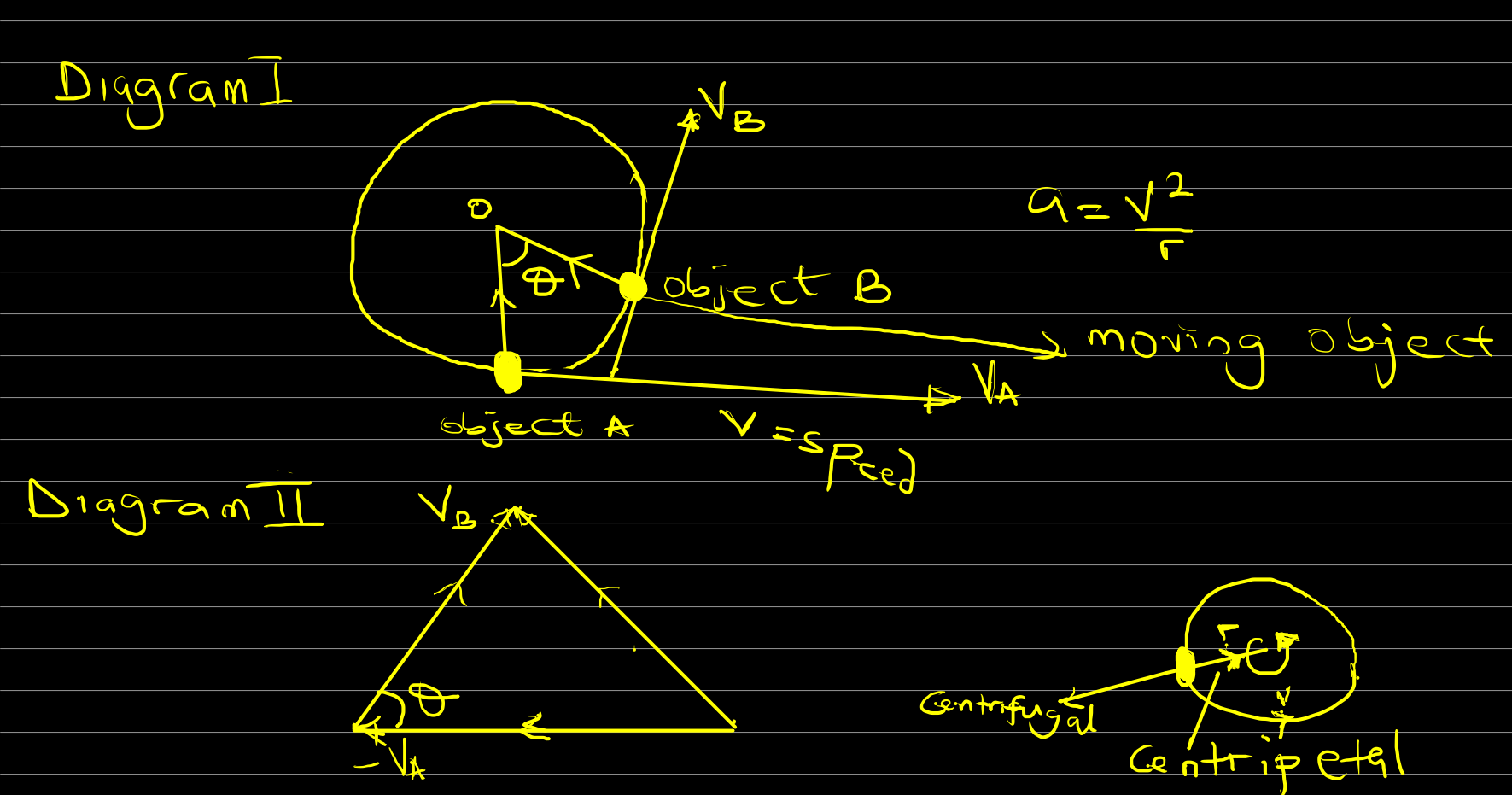
The change in velocity Δv is directed toward the center, and as such perpendicular, to v. Since the magnitude of the velocity at A and B are the same, despite their direction.
Therefore, the change in velocity Δv = vsinθ
as the angular change and the time to make the change is now smaller,
sinθ = θ
Therefore,
Δv = vθ
We need to also remember that acceleration is the change of velocity over time. Hence
a = Δv / t
Which will now become
a = vθ / t [Because Δv = vθ]
and the formula for angular velocity is ω = θ / t
Thus, we will now have
a = vω
and since v = ωr
We can write the formula for a as
a = ω2r or
a = v2 / r
How to Calculate Centripetal Acceleration
Here are a few solved problems:
Problem 1
A mass of 15 kilograms is moving in a circular path of radius 3 meters with a uniform speed of 30 meters per second. Find the centripetal acceleration of the object.
Solution
Data:
Mass, m = 15 kg,
Radius, r = 3 m, and
Uniform speed, v = 30 m/s
Centripetal accelaration, a =?
We can apply the formula that says a = v2/r
Therefore, we can now substitute our data into the above formula
a=v2/r = 302/3 = 900/3 = 300ms-2
Therefore, the centripetal acceleration of the body is 300 meters per second square (a=300ms-2).
Problem 2
A bus is traveling at a speed of 70 meters per second and is making a turn with a radius of 100 meters. What is the magnitude of the bus’ centripetal acceleration?
Solution
Data:
Speed, v = 70 m/s,
Radius, r = 100 m,
Centripetal acceleration, a =?
Since the formula for centripetal acceleration says a=v2/r
We can now say that
a=702/100 = 4,900/100 = 49ms-2
Hence, the centripetal acceleration of the bus is 49 meters per second square (a=49ms-2)
Problem 3
An airplane is flying in a circular path at a speed of 400 meters per second and a radius of 1000 meters. Find the centripetal acceleration of the airplane.
Solution
Data:
Speed, v = 400 m
Radius, r = 1000 m
Centripetal acceleration a=?
We can apply the formula a=v2/r to solve the problem
Hence, substitute our data into the above formula
a=v2/r = 4002/1000
Thus
a = 160,000/1000 = 160ms-2
Therefore, the centripetal acceleration of the airplane is 160 meters per second square (160ms-2)
Problem 4
A roller coaster makes a turn of 40 meters and a speed of 20 meters per second. Determine the centripetal acceleration of the roller coaster.
Solution
Data
The radius of the roller coaster, r = 40 m
Speed, v = 20 m/s
Centripetal acceleration, a =?
and the formula that will help us solve the problem is a=v2/r
After plugin our data into the above formula, we will get
a=v2/r = 202/60 = 400/40 = 10 ms-2
Therefore, the centripetal acceleration of the roller coaster is 10 meters per second square (10 ms-2).
Problem 5
A body moves along a circular path with a uniform angular speed of 0.7 rad/s and at a constant speed of 4.0 m/s. Calculate the acceleration of the body toward the center of the circle.
Answer
Data:
Angular speed, ω = 0.7 rad/s
v = 4.0 m/s
since v = ωr
Therefore, radius r = v / ω = 4 / 0.7 = 5.7 m
Hence, the acceleration toward the center is
a = v2 / r = 42 / 5.7 = 16 / 5.7 = 2.80 m/s2
Therefore, the acceleration toward the center of the circle is 2.8 meters per second square (m/s2)
NOTE:
Centripetal force (f) is defined as the force that tends to keep an object of mass (m), around a circular path of radius (r). The formula for centripetal force is f = mv2/r.
Centrifugal force is the reaction force that tends to move a body away from the center. In other words, it acts in opposite direction to the centripetal force which can be written as (- mv2/r).
A centrifuge is a device used to separate particles in suspension from the liquid in which they are contained. It consists of two tubes that are whirled by electrical means in a circle at a uniform speed. When you use the centrifuge, particles suspended in the less dense liquid would be observed to collect at the bottom of the centrifuge tube. It will leave the clear liquid at the top. While those in a denser liquid will collect at the top leaving the clear liquid at the bottom.
You may also like to read:
How to Calculate Centripetal Force
Reference
