Video Explanation of Moment of a Couple (M)
You can watch the full video explanation of the moment of a couple below:
For this topic, M represents the moment of a couple.
1. What is Moment of a Couple in Physics?
Definition: The moment of a couple is defined as the product of one of the forces (F) and the perpendicular distance (x) between the lines of action of the two forces.
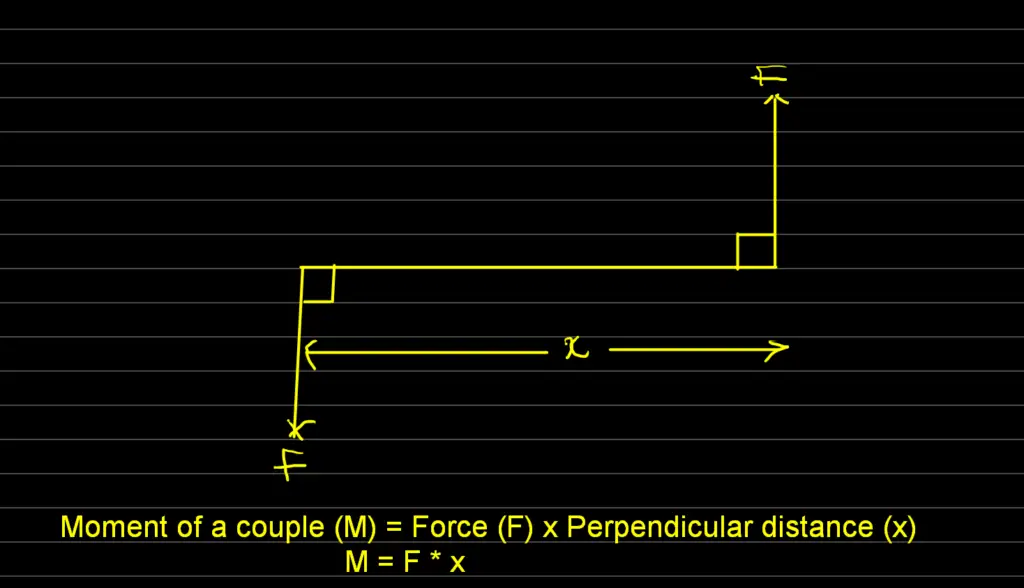
Additionally, the moment of a couple in physics refers to the rotational effect produced by two equal and opposite forces acting parallel to each other but not in the same line. It’s the product of one force’s magnitude, the distance between the forces, and the sine of the angle between the forces. The moment of a couple causes rotational motion without any translational motion.
SI Unit: The SI unit for the moment of a couple is the Newton meter (Nm).
Formula: The moment of a couple formula is given by: Moment (m) = Force (F) x Distance (x), where Force (F) represents one of the forces in the couple, and Distance (x) is the perpendicular distance between the forces.
Mathematically, we can write the formula as m = F * x.
| You may also like to read: |
| Equilibrium of Forces |
2. Explanation
To perfectly explain the moment of a couple in physics, imagine you and a friend are turning a wrench together. The moment of a couple is a bit like the teamwork needed to twist or rotate something without pushing or pulling it. It happens when two equal forces are applied in opposite directions and create a turning effect.
Picture turning that wrench: you and your friend apply forces in opposite directions, creating a rotational effect, or moment, around a point. The moment of a couple is like measuring how strong this turning effect is. It depends on the size of the forces and the distance between them.
Therefore, when you and your friend turn that wrench, the moment of the couple is what makes it spin. It’s a cool physics concept that helps us understand how things rotate without moving in a straight line, kind of like the magic behind turning a key or opening a door with a handle.
Solved Problems
Problem 1
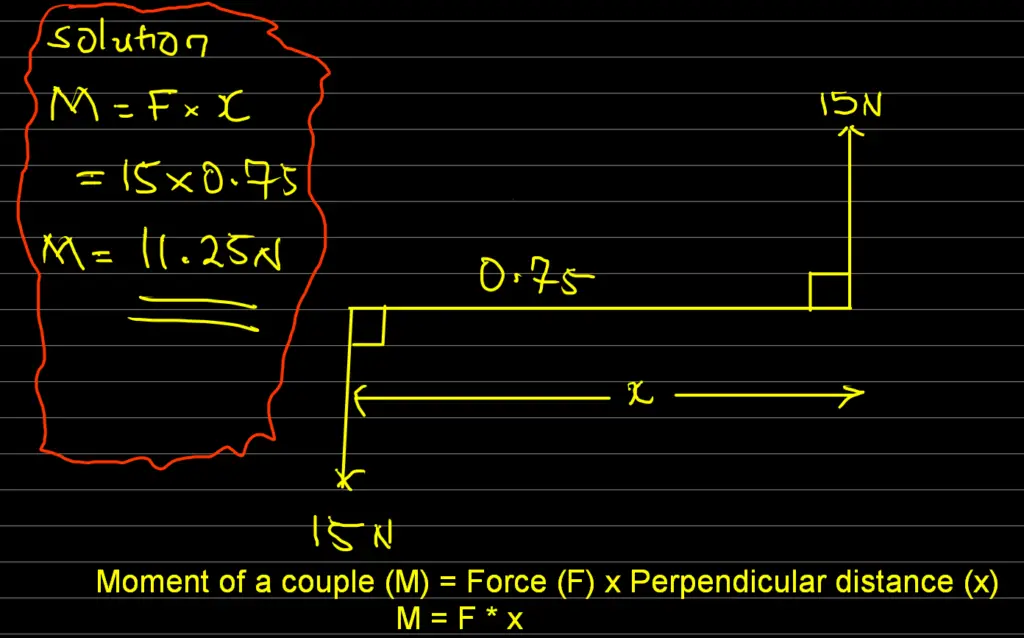
Calculate the moment of a couple in the figure above
Solution
Moment of a couple = One Force * Perpendicular distance between the forces
Therefore, M = F * x = 15 * 0.75 = 11.25 N
Therefore, the magnitude of the couple is 11.25 N
Problem 2
Two forces, each of magnitude 25 N, act in opposite directions at the opposite ends of a circular ring. If the diameter of the ring is 65 cm, calculate the magnitude of the couple acting on the ring.
Solution
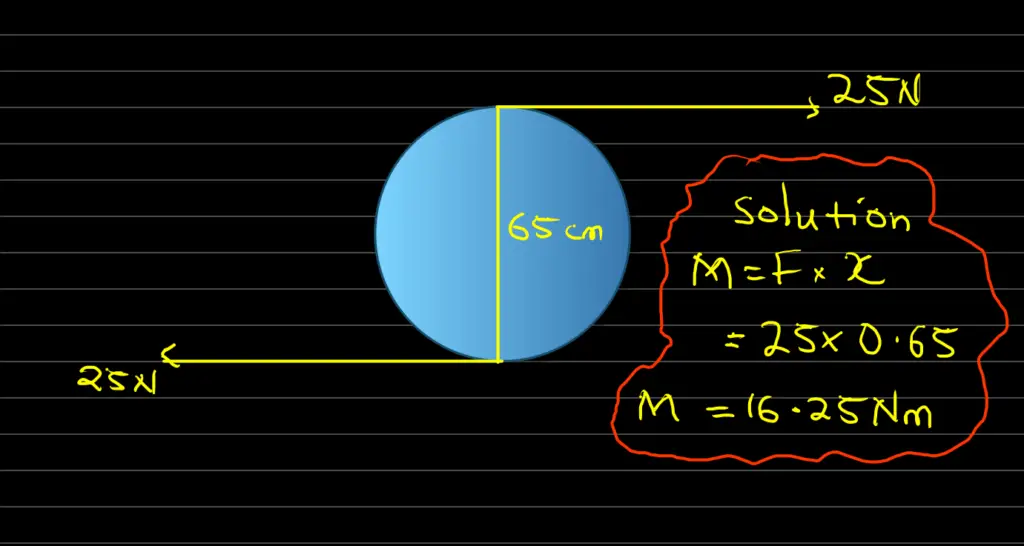
Moment of a couple (M) = Force (F) x Perpendicular distance (x)
Which means M = F * x = 25 N * 0.65 m = 16.25 Nm
Therefore, the magnitude of the couple acting on the ring is 16.25 Nm
| You may also like to read: |
| What is Young’s Modulus? |
3. Characteristics
Here are the characteristics of the moment of a couple:
- Equal and Opposite Forces: A couple involves two forces of equal magnitude acting in opposite directions.
- Parallel Forces: The forces in a couple act parallel to each other but have different lines of action.
- Rotational Effect: The primary characteristic is the creation of a rotational effect or moment without causing linear motion.
- Perpendicular Distance: The moment of a couple depends on the perpendicular distance between the forces’ lines of action.
- Independence: The rotational effect is independent of the point chosen for calculating the moment.
- No Net Translation: Couples do not produce a net translation or change in the object’s position.
- Vector Quantity: It’s a free vector
- Conservation: In an isolated system, the total moment of a couple remains constant unless external torques are applied.
- Torque Concept: M is conceptually similar to torque in rotational dynamics.
- Common in Mechanics: Couples are common in mechanical systems and help us to understand equilibrium and rotational motion.
| You may also like to read: |
| How to Find Resultant Force of Two Forces at an Angle |
5. Important Concepts
The moment of a couple in physics is a fundamental concept related to rotational motion. It is the measure of the rotational effect produced by two equal and opposite forces acting on a rigid body at different points parallel to each other. When we apply these forces at a specific distance from the axis of rotation, they create a rotational force, or torque, that tends to rotate the object.
We will now have a look at some of its key aspects:
a. Defining “Moment” and “Couple”
In physics, “moment” refers to the turning effect produced by a force about a particular point or axis. We can also refer to it as “torque.” A “couple,” on the other hand, is a pair of forces of equal magnitude and opposite direction that act on a body at different points.
b. Vector Nature of Moments
Moments, like forces, are vector quantities. This means they have both magnitude and direction. The direction of the moment is perpendicular to the plane containing the force and the axis of rotation.
c. Calculating the Moment of a Couple
We can calculate the M by multiplying one of the forces by the perpendicular distance (also known as the lever arm) between the forces. We use the formula M = F * x.
Where
- F is the force
- x is the perpendicular distance between the forces.
d. Moment of a Couple vs. Moment of a Force
It’s very important to distinguish between the moment of a couple and the moment of a single force. While the moment of a couple involves two forces, we calculate the moment of a force about a single point.
e. Principle of Moments
The principle of moments, also known as the law of moments, states that for an object in rotational equilibrium, the sum of the clockwise moments is equal to the sum of the anticlockwise moments.
f. Application in Everyday Life
The concept of this important topic has numerous applications in our lives. These applications range from the opening and closing of doors to the operation of wrenches and spanners, moments of couples are at work in various mechanical devices.
g. Angular Momentum and Conservation
M is closely related to the concept of angular momentum. Therefore, angular momentum is the rotational analogue of linear momentum, and just like linear momentum, angular momentum is conserved in a closed system.
h. Relationship with Center of Mass
M has a direct relationship with the center of mass of a system. Understanding this relationship will help us in solving physics problems involving stability and equilibrium.
| You may also like to read: |
| Dimension in Physics |
i. Moment of Inertia and Rotational Motion
The concept of the moment of inertia plays a significant role when studying the rotational motion of objects. Moment of inertia quantifies how mass is distributed about the axis of rotation.
j. Torque and Rotational Equilibrium
The concept of the M is tightly connected to the concept of torque. Torque is the rotational analogue of force, and it is important for understanding rotational equilibrium and rotational dynamics.
6. Examples of Moments of Couples in Physics
The moment of a couple in physics is not just a theoretical concept but one that finds practical applications in various real-life situations. Here are some examples of moment of couple:
a. Nut and Bolt Mechanism
When you tighten a nut and bolt, you apply equal and opposite forces in opposite directions on the bolt, creating a moment of a couple. Thus, this moment generates the necessary torque to secure the nut tightly.
a. Opening a Door
When you open a door, you apply force at the doorknob. The force is transferred to the hinges at the edge of the door, creating a moment of a couple that allows the door to rotate around its hinges.
c. Seesaw or Teeter-Totter
The seesaw is a classic playground equipment that exemplifies the concept of M. When children of different weights sit on opposite ends of the seesaw, their weights create opposing forces that balance each other, leading to rotational motion.
d. Pliers
We use pliers for gripping and manipulating objects. The two arms of the pliers work as a couple, generating the necessary force and torque to grip objects firmly.
e. Turning a Steering Wheel
When you turn the steering wheel of a vehicle, you are applying force at various points on the wheel, creating a MoC that steers the vehicle in the desired direction.
f. Swing Bridge Mechanism
Swing bridges are a type of movable bridge that rotates horizontally to allow boats to pass. We also use the same technique to operate the bridge, ensuring smooth rotation.
Frequently Asked Questions (FAQs)
Q: What is the primary significance of the moment of a couple in physics?
A: It helps us to understand rotational motion and equilibrium of rigid bodies. Additionally, it has practical applications in various mechanical devices and engineering systems.
Q: Can you explain the principle of moments in simple terms?
A: The principle of moments states that for an object in rotational equilibrium, the sum of the clockwise moments is equal to the sum of the anticlockwise moments.
Q: How is the moment of a couple related to angular momentum?
A: The angular momentum is the rotational analog of linear momentum, and both are conserved in a closed system.
Q: Is the moment of a couple always perpendicular to the plane containing the forces?
A: The moment is always perpendicular to the plane containing the forces and the axis of rotation.
Q: What is the difference between the moment of a couple and the moment of a force?
A: The moment of a couple involves two forces, while we calculate the moment of a force about a single point.
Q: How can I calculate the moment of a couple for a given system?
A: To calculate the M, multiply one of the forces by the perpendicular distance between the forces. You can simply apply the formula that says: M = F * x
You may also like to read: