What is Equilibrium of Forces?
Equilibrium in Physics: In physics, equilibrium is the state in which all forces acting on an object are balanced. It’s the key to understanding how objects behave when there are no unopposed forces acting on them. When an object is in equilibrium, the net force acting on it is precisely zero. In other words, all the forces are in perfect balance. Simply put, an equilibrium of forces is a situation when forces are placed at both ends of a body to stop it from moving or rotating (to balance its position). The force helps the body to remain in a balanced position.
Understanding Equilibrium of Forces
In physics, we usually say that the forces have cancelled each other so that the body can stay in EQUILIBRIUM.
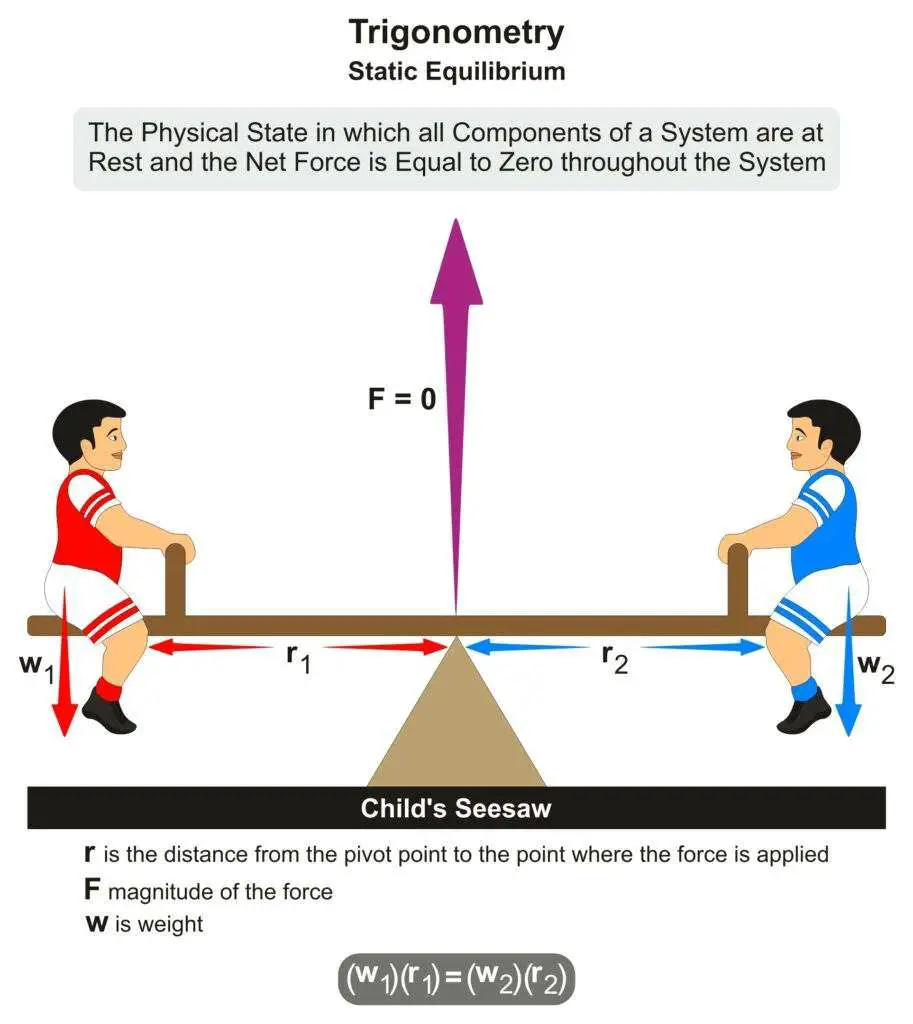
For example, when two children sit on the two ends of a seesaw. If the weight of both children is the same, the seesaw would remain in equilibrium.
But if their weight is not the same, the child with a higher weight would go down while a child with a lower weight would move up.
Another example of bodies in equilibrium is the tug-of-war game. Two groups of people are expected to hold a rope from both ends. The rope is separated by a line at the centre. For a group to win, they must pull the rope to make the other group cross into their line.
If both groups failed to pull each other, we can now say that they are at equilibrium and their forces have cancelled each other.
Therefore, for a body to remain at equilibrium, the net forces acting on the body must cancel each other.
The above explanation takes us to the statement: “The sum of the forces moving the body in one direction is equal to the sum of the forces pushing the body in the opposite direction”.
Additionally, for an object to remain in equilibrium, the vector sum of all relevant forces acting upon the object must be zero. Thus, the object cannot accelerate in an inertial frame of reference.
Forms of Equilibrium
We have three forms of equilibrium, and they are:
- Dynamic or Kinetic Equilibrium
- Static Equilibrium, and
- Thermal Equilibrium
Static Equilibrium
When forces acting on a body have the same magnitude and direction, they would help the body to remain at equilibrium.
Therefore, for a body to maintain static equilibrium, the sum of the forces acting on the body must be at rest. This implies that its net force is zero.
An Example of static equilibrium is a student bag sitting on the desk. The bag is pulled downward by gravitational force. At the same time, the desk exerts an equal and opposite force (upward force) to cancel the downward force of the bag.
The above example helps us to understand that the sum of the forces from both the bag and the desk is zero. Hence, they canceled each other so that the bag could remain on the desk.
In static equilibrium, the body is static and does not move. This is because all the forces acting on the body are the same.
Dynamic or Kinetic Equilibrium
In the case of dynamic equilibrium, the body moves with a constant velocity, and a zero net force or torque acting upon it.
The body undergoes translational motion with a constant velocity or rotates with a constant angular velocity about a fixed point.
Therefore, both forces that initiate and resist the motion are balanced.
For Example, a relationship between a car engine and a tarred road. The car engine helps the car to move on the tarred road, while the road resists the movement of the car. Consequently, the force of friction on the tarred road would try to oppose the movement of the car forward.
The two forces from the engine of the car and the friction of the tarred road will continue to cancel each other. Hence, both forces are in dynamic equilibrium.
The state of dynamic equilibrium helps the body to maintain constant velocity on the road. Your car will slow down if the friction is greater than the force of the engine. However, if the force of the engine is greater than the friction on the road, the car will accelerate.
Thermal Equilibrium
Temperature is the degree of hotness or coldness of a body. The coldness of a body signifies its low temperature, while the hotness of a body marks its high temperature. Therefore, when the temperature of a body rises from its lowest to a high degree, energy in the form of heat is transferred.
However, for a body to be in thermal equilibrium. The heat energy between the thermodynamic bodies must cancel each other. Hence, when the net flow of the heat energy is zero, the heat will stop flowing in the system.
State of Equilibrium
Here are some conditions for a body to be at equilibrium:
- The entire body remains at rest (motionless) or undergoes translational motion at constant velocity.
- The body either stops rotating or rotates at a constant angular velocity.
Resultant of Forces
When a body is under the influence of multiple forces, the resultant force is a force that when acting alone will have the same effect in magnitude and direction as the other forces acting together.
We use the symbol R to represent the resultant forces. Additionally, we apply the law of parallelogram to find the resultant forces.
When you have two forces A and B hanging at a point C. The resultant of the forces A and B at point C is calculated by applying the law of parallelogram.
The resultant of the two forces A and B have the same magnitude. However, the direction of forces A and B opposes the direction of the force at point C.
Balanced Forces and Their Role
The essence of equilibrium lies in balanced forces. An object is at equilibrium when the rightward forces are balanced by the leftward forces, and the upward forces are balanced by the downward forces. It’s essential to note that equilibrium doesn’t require all forces to be equal to each other. The critical factor is that these forces must balance each other.
Equilibrant of Forces
This is a force that cancels other forces. It has the same magnitude with resultant force, but they move in opposite directions.
To explain equilibrant, let’s assume we have three forces F1, F2, and F3 at equilibrium. The resultant of any two forces are equal but opposite in direction to one of the third forces.
Here is how it goes:
- The equilibrant of F1 and F2 is F3
- The equilibrant of F1 and F3 is F2
- The equilibrant of F2 and F3 is F1
Difference Between Resultant and Equilibrant Forces
| Resultant | Equilibrant |
| The resultant of two points acting at a point | It keeps a single force in equilibrium |
| The resultant of two forces acting from a source | A balanced force keeps different forces in a balanced state |
Principles of Triangle of Forces
The principle of the triangle of forces states that if three forces are in equilibrium, they can be represented in both magnitude and direction by the three sides of a triangle taken in order.
Moment of a Force
The moment is the turning effect of forces about an axis or point. The moment is the product of a force and the perpendicular distance of its line of action.
Principle of moment
The principle of moment states that if a body is in equilibrium, then the sum of the clockwise moments about any point on the body is equal to the sum of the anticlockwise moments about the exact point.
What is the Difference between Clockwise and Anticlockwise moments?
A clockwise moment is a rotational force that makes an object rotate in a clockwise direction. The anticlockwise moment is also a rotational force that makes an object rotate in the counterclockwise direction. The direction of rotation is determined by the direction of the force and the position of the object in relation to the force.
For example, we all know that a wall clock works by rotating in the right direction. Hence, when an object rotates in the direction of the clock, we say that it rotates in the clockwise direction.
The same scenario applies to anticlockwise moments. But in this case, the direction of the clock is assumed to rotate in the left direction. Thus, when an object’s rotation opposes the clockwise rotation. We can say that it moves counterclockwise or anticlockwise.
Couples
This is a pair of equal and parallel forces acting on a body in opposite directions and whose line of action does not meet. It produces the rotation of an object about a point.
Torque
The torque is the turning effect of a couple. It is the product of force and the perpendicular distance between the line of action of the two forces. Torque is a vector quantity and its unit is a newton-meter (Nm).
Parallel of Forces
Here are a few conditions for the equilibrium of rigid objects:
Under the action of Parallel forces
- The sum of the forces in one direction is equal to the sum of the forces in the opposite direction. Total downward force is equal to the total upward force.
- The sum of the clockwise moment of forces about any point is equal to the sum of the anticlockwise moment of the forces about the same point. The algebraic sum of the moment about any point is zero. It’s also important to know that the clockwise direction represents a negative sign while the anticlockwise moment represents a positive sign.
- The resultant force must be zero.
Under the Action of Non-Parallel Forces
- The line of action of the forces must coincide
- The resultant should be zero
- The algebraic sum of resolved components of the forces in any perpendicular direction is respectively zero.
Three Non-Parallel Coplanar Force
- If any object is in equilibrium under the actions of three forces, the resultant of the two forces must be equal and opposite to the third force.
- The lines of action of the forces must coincide at a point.
- All three forces must coincide.
- The third force’s line of action must go through the point where the lines of action of the other two forces intersect.
- The sum of the forces at a point must add up to zero.
- The forces can be represented in a magnitude and direction by the sides of a triangle taken in order.
Centre of Gravity
This is a point through which the resultant weight of the body appears to concentrate. We can also define center of gravity as the point at which the weight of a body acts, regardless of the body’s position.
Types of Equilibrium
There are three types of equilibrium:
- Stable Equilibrium: A body regains its original position after slight displacement. A large bottom and a low center of gravity would make an object maintain a stable equilibrium. A television on a TV stand is stable if it does not fall. When a body is unlikely to be upset by a small movement, we say that the body is stable.
- Unstable Equilibrium: A body moves further away from its equilibrium position when slightly displaced. The body does regain its original position.
- Neutral Equilibrium: A body comes to rest in its new position. For example, when an object like a cylinder is pushed to the ground. The center of gravity of that cylinder does not change.
Equilibrium of Bodies in Liquids
When you carry a bucket that is filled with water, you will definitely feel the effect of its weight. However, when you pull the same bucket with an exact quantity of water from a well. You will realize that it is not as heavy as it was in the air.
The lightness of the bucket while in the water is due to a force that pushes the bucket in an upward direction. The force will try to cancel the weight of the object that is pushing it downward. The force is called upward force or upthrust.
Upthrust
When a body is fully or not entirely immersed in a liquid, it will face an ascending force. We can also define an upthrust as the reaction force exerted on a body when wholly or partially immersed in a fluid.
If the weight of the bucket in air is W2, and the weight of the bucket while immersed in the water is W1. Then, the upthrust on the bucket is
Upthrust, U = Weight in air (W2) — Weight in the water (W1)
Additionally, we can find the weight when immersed in the water by making W1 subject of the formula in the above equation
Weight in the water (W1) = Weight in air (W2) — Upthrust, U
We can also apply the following formula to calculate the upthrust of an object:
Upthrust = volume of the object x density of the liquid x gravitational acceleration
Upthrust = (V/3) x density of liquid x g
Archimedes Principle
Archimedes’ principle states that when a body is partially or wholly immersed in a fluid, the upthrust on the body is equal to the displaced weight of the liquid.
Upthrust = Displaced weight of the liquid
And the above expression will give us
Upthrust = volume of the object (v) x density of the liquid (ρ) x gravitational acceleration (g)
Therefore, the upthrust is
Upthrust = vρg
Principle of Floatation
The principle of floatation states that when a body is totally or partially immersed in a fluid, its weight is equal to the weight of the displaced fluid. Examples of bodies that float are ships and ice.
Density and shape are some of the important factors that will help the body to float.
Weight of the body floating = weight of the displaced fluid
Calculations for Equilibrium of Forces
Here are a few calculations of the equilibrium of forces to improve your understanding of the topic:
Problem 1
Two forces of 5 newtons each are inclined at an angle of 120 to each other. Find the single force that will:
- Replace the given force system
- Balance the given force system
Data
Two forces are equal = F1 and F2 = 5 N
Angle,θ = 1200
Formula
To find the single force that will replace the given force system, we will apply the formula
R2 = F12 + F22 + 2F1F2Cosθ
Solution
We can insert our data into the formula to solve the problem
R2 = 52 + 52 + 2 x 5 x 5 x Cos1200 = 25 + 25 + 20 x (- cos600)
We can now rewrite the above expression as
R2 = 50 – 20 x 0.5 = 50 – 10 = 40
Hence, R = √40 = 6.32 N which can be approximated to 6 Newtons
Therefore, the resultant force is 6 N.
R = 6 n
We can now apply the sign rule to obtain α
(6/sinα) = (R/sin600) = (6/sin600)
This is now equal to
Rsinα = 6sin600
This implies that
6sinα = 6sin600
and we have
sinα = sin600
which can be written as
α = sin-1 [sin600]
Therefore,
α = 600
b. Equilibrant = 6 N
Problem 2
A meter rule is pivoted at its midpoint C with a vertical force of 10 newtons hanging from a distance of 30 centimeters from C. At what distance must a 15 Newton force hang to balance the ruler horizontally?
Data
Vertical force, F1 = 10 N
Distance from the side of F1, S1 = 30 cm
Force on the other side, F2 = 15 N
Unknown value
Distance on the same side of F2, S2 = ? (we can use S2 to find the unknown)
Formula
The formula we need to apply is
F1S1 = F2S2
Solution
add your data into the formula to get
10 x 30 = 15 x S2
we can now make S2 subject of the formula
S2 = 300/15 = 20 cm
Problem 3
A boy of mass 10.0 kilograms sits at a distance of 1.5 meters from the pivot of a seesaw. If another boy of mass 20.0 kilograms sits at a distance of 1.0 meters from the pivot, will the seesaw balance horizontally?
Solution
Moment at 10 kg = 100 N
The moment of 100 N force about C = 100 x 1.5 = 150 N
Moment at 20 kg = 200 N
The moment of 200 N force = 200 x 1 = 200 N
The seesaw will tilt in the direction of the 20 kg boy.
Problem 3
A piece of cork density 0.25 x 103 kilograms per meter cube floats in a liquid of density 1.25 x 105 kgm-3, what fraction of the volume of the cork will be immersed? [GCE]
Solution
Total volume of the cork = V1
The volume of the submerged cork = V2
Initial density at V1 = 0.25 x 103 kgm-3
Final density at V2 = 1.25 x 105 kgm-3
Mass of the cork = volume x density
Thus
V1 x 0.25 x 103 = V2 x 1.25 x 105
To find the ratio, we say
V1/V2 = (0.25 x 103)/(1.25 x 105)
Hence
V1/V2 = 1/5 = 0.2
Practical Applications
1. Sign Analysis:
Now, let’s move from theory to practical applications. A common scenario where equilibrium principles are applied involves the analysis of signs hanging on walls. Consider a picture hanging on a wall. This picture is in a state of equilibrium, meaning all forces acting upon it must be balanced. In practical terms, this means that all horizontal components of the forces must add up to zero, and all vertical components must also sum to zero. This analysis is crucial for ensuring that the picture remains securely in place.
2. Determining Weight:
But how do you determine the weight of the picture hanging on the wall? To answer this question, one can conduct a force analysis using trigonometric functions. The weight of the sign is the sum of the upward components of the tension in the two cables. This vertical component can be determined using trigonometry.
3. The Role of Trigonometry:
Trigonometry plays a significant role in understanding equilibrium. When forces act at angles, trigonometric functions help resolve these forces into their horizontal and vertical components. By calculating these components, we can determine if the vertical and horizontal forces are balanced. This is a powerful tool in equilibrium analysis, as it allows for precise measurements and predictions.
Analyzing Tension and Angles
The Relationship Between Tension, Angle, and Weight: One of the key relationships to grasp is how tension, angle, and weight are interconnected. The tension in cables and the angle at which the cables make with the horizontal are vital factors. Knowing any two of these values allows you to calculate the third using trigonometric functions.
Variation of Tension with Angle: Understanding how tension varies with the angle is a fundamental concept. As the angle with the horizontal increases, the amount of tensional force required to hold the object at equilibrium decreases. This principle is vital in various engineering and real-world applications, as it impacts the design and stability of structures.
Key Principles of Equilibrium
Summary of Fundamental Concepts: To summarize, equilibrium is a state in which all forces acting upon an object are balanced, resulting in a net force of zero Newton. This condition is crucial for understanding and predicting how objects behave. Equilibrium allows us to analyze forces and predict the behavior of structures and objects in diverse scenarios.
The Role of Trigonometry: Trigonometry is an indispensable tool in equilibrium analysis. It helps resolve forces into their components, making it possible to determine if the vertical and horizontal forces are in balance. Whether it’s determining the weight of a sign or analyzing complex structures, trigonometry enables precise calculations.
You may also like to read:
How to Calculate the Relative Density of a Liquid
How to Calculate the Resultant of Two Forces at an Angle