What is a Position in physics?
Definition of position in physics: Position in physics simply means the location of an object in a plane or space. We can determine the position of an object by considering it is distance and direction from a specific frame of reference. Therefore, this is to say that we can find the position of an object, once we know its distance and direction from a specific point of reference.
The location of your television stand in your room is the position of that television stand. The location of your school from your home is the position of that school. A football coach wants his players to occupy a specific position on the field during a match competition. A man driving a car occupies a certain position as he continues to move.
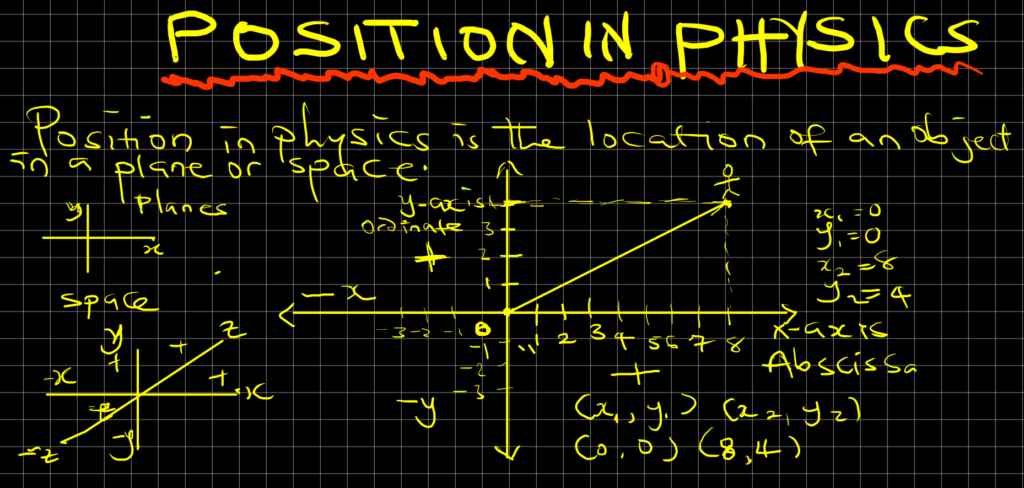
Therefore, finding the position of an object is very important. To find the position of an object, we need to consider the x and y coordinates on a plane. In simple terms, we need to draw two lines that meet each other in the middle (we call it origin), and make sure that the two lines are perpendicular to each other.
We start measuring the position of an object from the origin of that object on a plane. The origin of an object on an x-y plane is the point where it starts from zero, it is the reference point where the object is seen or observed.
The vertical reference line is along the y-axis, while the horizontal reference line is along the x-axis.
To find the position of an object, we need to understand whether it belongs to a space or a plane.
A Plane
A plane is due to two frames of reference, in form of an x and y-axis. We have two coordinates on a plane, the x-coordinate is known as abscissa, while the y-coordinate is known as ordinate. The horizontal component consists of the right and left sides starting from the origin. When you start from the origin and move to the left, it means that you are moving along the negative x direction.
When you start from the origin of the horizontal plane and move to the right, it means that you are heading toward the positive direction of the x-axis.
We also have a vertical component of the plane called the y-axis. The origin intersects the y-axis at the middle making the upper side a positive side of the y-axis, and the lower side a negative y-axis.
A plane is in the form of (x,y) coordinate.
A space
Space consists of a three-dimensional coordinate system. We can find the location of an object in space by considering (x,y,z) coordinates. We have three coordinates in space, and they are x, y, and z.
How to Find a Position in Physics
Let’s assume we are dealing with a plane in form of x-y coordinates. We write an ordered pair of values as (x,y). We measure values on a vertical line along the y direction, and we also measure values on the horizontal line which is the x direction.
Assuming the position of an object is on a plane (5,7) as our values, here is how to find the position of the object on a plane.
- Starting from the origin (zero), count 5 units along the positive x-axis
- Additionally, count 3 units along the positive y-axis
- On the vertical line, draw a horizontal line starting from 7 units and move toward the right.
- on the horizontal axis, draw a line starting from 5 units and move upward until the two lines intersect
- Draw a line from both axis so that they meet at the center (5,7)
- Let’s assume we have A(x1,y1,z1) and B(x2,y2,z2)
- To calculate the distance between A and B
- We apply the formula AB2 = (x2 – x1 )2 + (y2 – y1 )2 + (z2 – z1 )2
- Additionally, to find the direction of AB. We apply [ tanθ=Opposite/Adjacent ]
Examples of Position in Physics
Here are some examples to guide you on finding an object’s position in a plane or a space.
Example 1
Calculate the distance between two points M (5,6) and N (12,8) on a plane.
Solution:
Data
We can see that the coordinates belong to a plane in the form of (x,y).
Therefore, from the question:
x1 = 5
x2 = 12
y1 = 6
y2 = 8
MN2 = (x2 – x1 )2 + (y2 – y1 )2
We now substitute our data into the above formula
MN2 = (12 – 5 )2 + (8 – 6 )2
After squaring the right-hand side, we have
MN2 = 72 + 22
which is equal to
MN2 = 49 + 4
Now, we sum up our right-hand side(RHS)
MN2 = 53
By making MN the subject of the formula, and transferring the square to the RHS so that it can become the square root
MN = √53 = 7 units
our final answer is now
MN = 7 units
Example 2
What is the distance between P(3,5,7) and Q(-4,4,-3)
Solution
Data
From the above question, we have our data as follows:
x1 = 3
x2 = -4
y1 = 5
y2 = 4
z1 = 7
z2 = -3
Now we apply the formula that says
PQ2 = (x2 – x1 )2 + (y2 – y1 )2 + (z2 – z1 )2
By substituting our values into the above equation, we now have
PQ2 = (-4 – 3)2 + (4 – 5)2 + (-3 – 7)2
This is now equal to
PQ2 = (-7)2 + (- 1)2 + (-10)2
Thus, it is now
PQ2 = 49 + 1 + 100
After summing the right-hand side, it becomes
PQ2 = 150
we now take the square root of both sides to eliminate the square on the left-hand side
√PQ2 = √150
This is now equal to
PQ = √150 = 12.3 units = 12 units
Example 3
Two players were perfectly positioned at A(2,3,5) and B(6,0,8)
a. Determine the distances OA and OB if O is the point in a field represented by O(1,0,2)
b. Find the distance between the two players, BA
Solution
Data:
By extracting our data from the above question, we have
Point A(2,3,5) and B(6,0,8) with an origin O(1,0,2)
and if O(x1,y1,z1), A(x2,y2,z2) and A(x3,y3,z3)
Thus,
x1 = 1, x2 = 2, and x3 = 6
y1 = 0, y2 = 3, and y3 = 0
z1 = 2, z2 = 5, and z3 = 8
a. To find OA, we apply the formula
OA2 = (x2 – x1 )2 + (y2 – y1 )2 + (z2 – z1 )2
By inserting our data into the above equation, we will have
OA2 = (2 – 1)2 + (3 – 0)2 + (5 – 2)2
This is equal to
OA2 = 12 + 32 + 32
After squaring the right-hand side(RHS), it becomes
OA2 = 1 + 9 + 9
We now add the values in the RHS and then apply the square root to both sides in order to make the OA subject of the formula
OA = √19 = 4.4 = 4 units
Therefore, the distance OA is 4 units or 4 meters
To calculate OB, we apply the same method for OA
Thus
OB2 = (x3 – x1 )2 + (y3 – y1 )2 + (z3 – z1 )2
after substituting our data into the above formula for calculating distance, we now have
OB2 = (6 – 1)2 + (0 – 0)2 + (8 – 2)2
This is equal to
OB2 = (5)2 + (0)2 + (6)2
we will now have
OB2 = 25 + 0 + 36
after summing up the RHS, we now have
OB2 = 61
by making OB the subject of the formula
OB = √61 = 7.8 = 8 units
Therefore, the distance between OB is 8 units or 8 meters.
b. To Find the distance between the two players A and B, we apply the formula
AB2 = (x2 – x3 )2 + (y2 – y3 )2 + (z2 – z3 )2
After substituting our data into the above equation, we will have
BA2 = (x3 – x2 )2 + (y3 – y2 )2 + (z3 – z2)2
Thus,
BA = √[(6 – 2)2 + (0 – 3)2 + (8 – 5)2]
We now have
BA = √[(4)2 +(- 3)2 + (3)2]
it will now become
BA = √16 + 9 + 9
Thus,
BA = √16 + 9 + 9 = √34 = 5.8 = 6 units
Therefore the distance between the two players, BA is 6 units or 6 meters
You may also like to read:
SS1 Lesson Note: Introduction to Physics For First Term
Reference:
