Concept of Velocity Ratio (V.R)
In this post, you will learn how to calculate the velocity ratio of an inclined plane. Before we start solving problems, we need to understand the definition of velocity ratio.
What is the velocity ratio? Velocity ratio is the ratio of the distance covered by an effort to the distance covered by the load in the same time interval.
We also refer to the velocity ratio of an inclined plane as vr of inclined plane.
What is the Velocity Ratio of an Inclined Plane?
The velocity ratio of an inclined plane is the ratio of the effort’s velocity to the load’s velocity, allowing easier movement of loads along the slope compared to vertical lifting (along an inclined plane).
The velocity ratio of an inclined plane represents the advantage gained in moving a load along its length compared to lifting it vertically. It is the ratio of input force (effort) to output force (load) velocities, making it easier to move heavy objects by applying a smaller force over a longer distance.
Additionally, the velocity ratio of an inclined plane does not have a unit. It is a dimensionless quantity that expresses the mechanical advantage gained in using the plane to move a load compared to lifting it vertically.
Velocity Ratio of Inclined Plane Formula
We can express the velocity ratio (v.r) formula in mathematical form as
Velocity Ratio (V.R) = Distance of the Effort / Distance of the Load
V.R rely on the geometry of the machine
For an inclined plane, the machine will assist us in pushing bodies up an inclined plane with ease. We apply an inclined plane to push heavy objects up a slope.
Velocity ratio (V.R) = length of plane / height of a plane = L/h
Thus
Sin θ = h/L
Therefore, we can say that
V.R = 1 / Sin θ
How to Find Velocity Ratio of an Inclined Plane
To find the velocity ratio of an inclined plane:
- Measure the length of the inclined plane (effort distance) and the vertical height it covers (load height).
- Calculate the ratio: Velocity Ratio = Effort Distance / Load Height.
- The result indicates how much easier it is to move a load along the plane compared to lifting it vertically.
Solved Problems: How to Calculate the Velocity Ratio of an Inclined Plane
Here are a few problems to help us understand how to calculate the velocity ratio of an inclined plane:
Problem 1
Calculate the velocity ratio of an inclined plane which makes an angle of 600 with the horizontal.
Solution:
Data:
From the question above, we are to calculate the V.R which is unknown to us
Therefore V.R = ?
Angle (θ) = 600
and the mathematical expression for V.R = 1 / Sin θ
and θ = 600
Which implies
V.R = 1 / Sin 600
and Sin 600 = 0.866
This implies that
V.R = 1 / 0.866
Thus,
V.R = 1.15
Therefore, the velocity ratio of an inclined plane which makes an angle of 600 to horizontal is 1.15
This is a very simple example of how to calculate the velocity ratio of an inclined plane
Problem 2
A floor of a lorry is 2.0 m high. A plank 5 m long is used as an inclined plane to raise some load up the lorry. If the efficiency of this machine is 50% what is the minimum effort (applied parallel to the plane) required to raise 200 N load up the plane?
Solution
Data:
We need to gather our data to be able to solve the problem
Firstly, we can see from the question that the effort required to raise the load = length of the plank = 5 m
Additionally, the distance moved by the load = floor of the lorry = 2.0 m
Efficiency = 50%
Load = 200 N
From the above data, we apply the formula
Velocity Ratio (V.R) = 1 / Sin θ = Distance moved by effort = Distance moved by load
V.R = 5 / 2 = 2.5
Also
Efficiency = ( M.A / V.R ) x 100%
By substituting our data into the above equation and the solution for V.R we have
50% = ( M.A / 2.5 ) x 100%
by making M.A the subject of the formula, we have
( 50% / 100% ) x 2.5 = M.A
Therefore
M.A = 0.5 x 2.5 = 1.25
Now we can write
M.A = Load / Effort
To find Effort, we make it the subject of the formula from the above equation
Effort = Load / M.A
This implies
Effort = 200 / 1.25 = 160 N
Problem 3
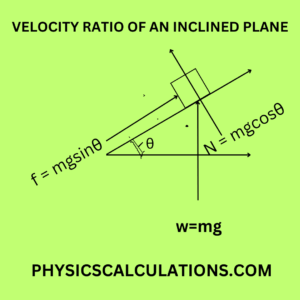
A block of mass 2 kg is placed on an inclined plane whose angle of inclination is increased until the block is just about to slide down the plane. If the angle of inclination of the plane is 600 at this point, calculate the force, parallel to the plane which will just move the block up the inclined plane.
Solution
Data:
We deduce our data by looking at the question above
Assuming the required Force = P
There is also a force resisting the movement of the load up to the inclined plane which is
Fictional force on the plane F = μR
We also have a Reactional Force R = wcosθ
and we also have a force acting down the plane, which is force = wsinθ
w = weight = mg
Therefore, the total force acting down the plane is
T = μR + wsinθ
T = μmg cos θ + mg sin θ
We should also know that limiting friction μ = tan θ
Now, T = tan θ mg cos θ + mg sin θ
Since θ = 600 , m = 2kg , and g = 10 ms-2
We have
T = tan 600 x 2 x 10 x cos 600 + 2 x 10 sin 600
T = 1.73 x 20 x 0.5 + 20 x 0.866
Therefore
T = 34.64 N
Problem 4
An effort of 20N is applied to lift a load of 120N with the aid of a machine. The distances covered by the effort and the loads are 50 meters and 200 meters respectively. Calculate the velocity ratio of the machine.
Solution:
Data: You need to extract your data from the question to simplify your work.
-Underline the figures
-take note of the s.i units
-relate the figures with the corresponding parameters
-apply the v.r formula to solve the problem
Now,
V.R = ?
Distance moved by the effort = 50 meters
Distance moved by the load = 200 meters
The formula for Velocity ratio (V.R) = Distance moved by the effort (50 m) / Distance moved by the load (200 m)
V.R = 50 / 200 = 0.25
Problem 5
A 20-kilogram mass is to be pulleyed up a slope inclined at 300 to the horizontal. If the efficiency of the plane is 75%, calculate the force required to pull the load up the plane.
Solution:
Data:
Load, L = 20kg = 200N
The angle, θ = 300
Efficiency, η = 75% = 75/100 = 0.75
The force required to pull the load up an inclined plane = Effort = E = ?
Now we apply the formula that says
V.R = 1 / Sin θ
Which implies that the velocity ratio of an inclined plane is
V.R = 1 / Sin 300
Thus,
The velocity ratio of an inclined plane, V.R = 1/0.5 = 2
Additionally, the mechanical advantage, M.A = Load / Effort = L / E = 200 / E
But the formula for efficiency is η = ( M.A / V.R ) x 100%
By substituting our values into the above formula for efficiency, we have
75 = [ (200/E) / 2 ] x 100
this is equal to
75/100 = (200/E) / 2
0.75 x 2 = 200/E
1.5 = 200 / E
Thus, E = 200 / 1.5 = 133.3N
Problem 6
A body of mass 7.5 kilograms is to be pulled up along a plane that is inclined at an angle of 30 degrees to the horizontal. If the efficiency of the plane is 75%, Calculate the velocity ratio of the plane.
Solution:
Data:
mass, M = 7.5kg
Angle of inclination, θ = 300
Efficiency, η = 75% = 75/100 = 0.75
The velocity ratio of an inclined angle is V.R = 1 / Sin θ
Thus
V.R = 1 / Sin 300 = 1 / 0.5 = 2
Problem 7
A man pulls up a box of mass 70 kg using an inclined plane of an effective length 5 meters onto a platform 2.5 meters high at a uniform speed. If the frictional force between the box and plane is 100N. Calculate the velocity ratio of the angle of inclination.
Solution
Data:
Since Sin θ = opposite / hypotenuse
and we can see that opposite length = 2.5m
Hypotenuse = 5m
Thus
Sin θ = 2.5 / 5 = 0.5
Now we can write the above expression as θ = Sin-1 0.5
Thus θ = 300
Applying the formula for the velocity ratio of an inclined plane (V.R = 1 / Sin θ), we now have
V.R = 1 / Sin 300 = 1 / 0.5 = 2
Thus the velocity ratio of an inclined plane is 2
Problem 8
A box of weight W resting on a plank PQ that has it is lower end P hinged to a horizontal floor PR. The plank makes an angle θ to the floor. If the box is pulled up from P to Q, what is the expression for the velocity ratio of an inclined plane?
Solution
Data:
Distance covered by the effort = PQ
Distance covered by the load = QR
We know that the velocity ratio (V.R) of an inclined plane
V.R = distance covered by the effort/distance covered by the load
This implies that
V.R = PQ / QR
Problem 9
An object is released from the top of an inclined plane about 250 meters long and 50 meters high. What is the velocity ratio of the inclined plane?
Solution
Data
After reading the above question, we can come up with our data as follows:
Length of the plane, L = 250 meters
Height of the plane, h = 50 meters
Now, apply the formula for the velocity ratio below to find our answer
We initially said that Velocity ratio (V.R) = length of the plane (L)/height of a plane (h) = L/h
Thus, we can easily insert our data in the above formula velocity ratio of an inclined plane to represent the length of the plane (L) and height of the plane (h).
Therefore,
V.R = L/h = 250/50 = 5
Hence, the velocity ratio of the inclined plane is 5 [Note: Velocity ratio does not have a unit]
Problem 10
Five laborers allowed a drum to roll along a horizontally inclined tower about 2 kilometers long and 500 meters high. Calculate the velocity ratio of the inclined tower.
Solution
Data
The length of the tower, L = 2 km = 2 x 1000 meters = 2000 meter
Height of the tower, h = 500 meters
We can now calculate the velocity ratio of the inclined tower by applying the formula that says
We initially said that Velocity ratio (V.R) = length of the plane (L)/height of a plane (h) = L/h
Thus,
V.R = L/h = 2,000 meters / 500 meters = 4
Therefore, the velocity ratio of the inclined tower is 4
Problem 11
A body is released from the top of an inclined plane 150 meters long and 25 meters high. Find the velocity ratio if the angle of inclination is thirty degrees (300).
Solution
Data
Start by extracting your data from the question
Length of the plane, L = 150 meters
Height of the plane, h = 25 meters
We have two scenarios in this question. We need to apply the formula that says V.R = L/h to solve the problem, and then apply the other formula that was affected by the angle of inclination (slope). You can then multiply the two to obtain the total velocity ratio of the plane.
Applying V.R = L/h
Now, apply the formula for the velocity ratio below to find our answer
We initially said that Velocity ratio (V.R) = length of the plane (L)/height of a plane (h) = L/h
Therefore, V.R = 150 meters / 25 meters = 6
Applying V.R = 1 / Sin θ
To calculate the velocity ratio of an inclined plane formed by an angle of 300, we apply the formula, V.R = 1 / Sin θ
Thus
V.R = 1 / Sin 300 = 1 / 0.5 = 2
We can now multiply the two velocity ratios to arrive at the total velocity ratio of the plane
V.R = 2 x 6 = 12
Therefore, the velocity ratio of the plane is 12
Problem 12: For an inclined plane derive efficiency=l/h
For an inclined plane derive efficiency=l/h
Solution
Certainly! To derive the efficiency (( \eta )) of an inclined plane, which is defined as the ratio of useful work output (Wout) to the total work input (Win), you can follow these steps:
- Useful Work Output (Wout): When an object is moved along an inclined plane, the useful work done is the weight of the object (Fload = m x g) multiplied by the distance it moves horizontally (l). Therefore, Wout = Fload x l.
- Total Work Input (Win ): The total work done on the object is the applied force Feffort multiplied by the distance it moves horizontally (l). Thus, Win = Feffort x l.
- Efficiency (η) Calculation: Divide the useful work output by the total work input and express it as a fraction: η = Wout / Win = (Fload x l) / (Feffort x l) = Fload / Feffort
- Substitute Load and Effort Forces: In terms of load Fload and Feffort forces along the inclined plane, you can use trigonometry: Fload = Feffort x Sinθ, where θ is the angle of inclination.
- Final Expression: Substituting the load-force relationship into the efficiency equation: η = Fload / Feffort = (Feffort x Sinθ) / Feffort. Now, we can relate Sinθ to the ratio of load height (h) to the inclined plane length (l) using trigonometry: Sinθ = h/l. Thus, the derived efficiency of the inclined plane is: η = h/l
This demonstrates that the efficiency of an inclined plane is directly proportional to the ratio of the load height to the inclined plane length.
Frequently Asked Questions (FAQ) on the Velocity Ratio of an Inclined Plane
- What is the velocity ratio of an inclined plane?
The velocity ratio is the ratio of the length of the inclined plane (L) to the distance it would have traveled if it had fallen through the same distance in a vacuum (height of the plane).
2. How to calculate the velocity ratio of an inclined plane?
Calculating the velocity ratio depends on the nature of the question you are dealing with. Here are two methods to calculate the velocity ratio of an inclined plane:
a. When you are dealing with an angle, apply the formula that says the velocity ratio is V.R = 1 / Sin θ
b. You can also apply the formula, V.R = Length of the plane (L)/Height of the plane (h)
3. Mention Two Factors that Affect the Velocity Ratio of an Inclined Plane
a. Coefficient of friction between the angle of inclination and the body
b. Angle of inclination
4. Is it Possible for the Velocity Ratio of an Inclined Angle to be Greater than One?
If the coefficient of friction is low, while the angle of inclination is high. Then the velocity of an inclined plane can be greater than 1.
5. What do You Understand by the Relationship Between the Velocity Ratio of an Inclined Plane and the Mechanical Advantage of a Machine?
The velocity ratio is inversely proportional to the mechanical advantage of a machine.
You may also like to check:
How to Derive the Formula For Increase in Volume
Check our websites:
Wokminer – Search and apply for a job
