Question
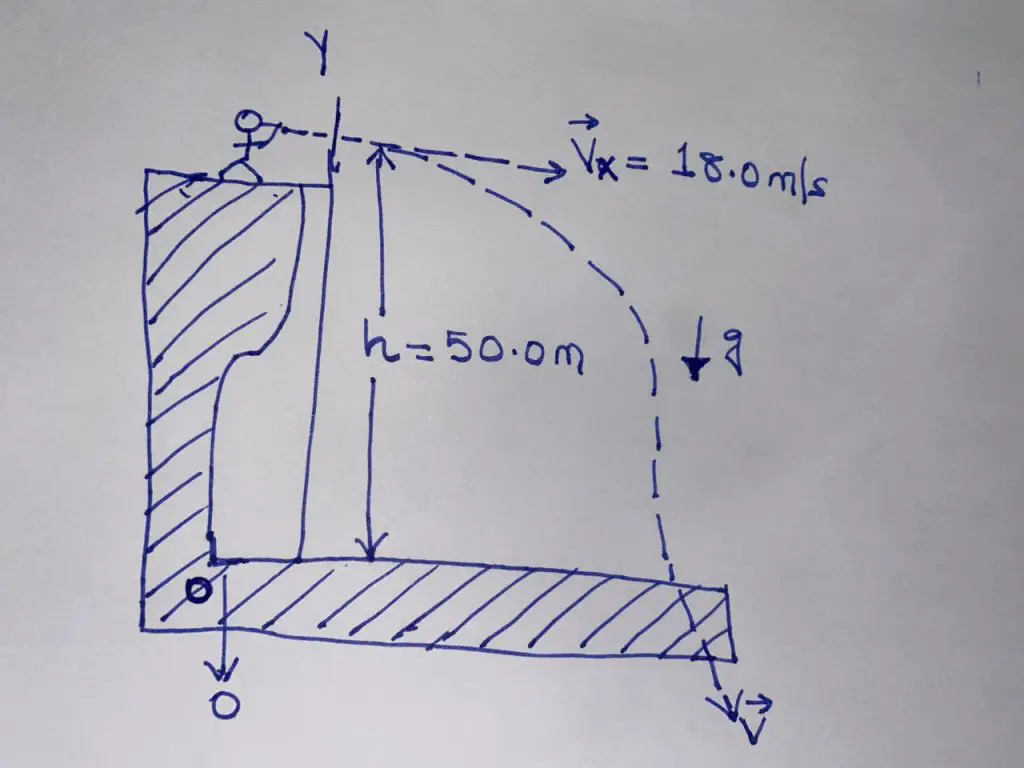
A student stands at the edge of a cliff and throws a stone horizontally over the edge with a speed of 18.0 m/s. The cliff is 50.0 m/s above the flat, horizontal beach as shown in the figure.
a. What are the coordinates of the initial position of the stone?
b. What are the components of the initial velocity?
c. Write the equations for the x and y components of the velocity of the stone with time, using the coordinates in the figure below.
d. How long after being released does the stone strike the beach below the cliff?
e. With what speed and angle of impact does the stone land?
Final Answer
Therefore, the stone strikes the beach with a speed of approximately 36.06 m/s at an angle of 60.40 below the horizontal.
Explanation
(a): Coordinates of the Initial Position of the Stone
Assuming the initial position of the stone is at the edge of the cliff, we can set the origin of our coordinate system at the base of the cliff. Thus, the coordinates of the initial position of the stone would be:
(x0, y0) = (0, 50.0m)
(b): Components of the Initial Velocity
The stone is thrown horizontally, so the initial velocity has only an x-component and no y-component. Given the initial speed:
v0x = 18.0 m/s
v0y = 0
(c): Equations for the x and y Components of the Velocity of the Stone with Time
For the x-component (horizontal motion):
Since there is no horizontal acceleration (assuming no air resistance): vx (t) = v0x = 18.0 m/s
For the y-component (vertical motion):
Since the stone is in free fall, it is subject to gravitational acceleration or negative acceleration, g = – 9.8 m/s2
vy (t) = v0y + gt = 0 + (- 9.8) x t = – 9.8t m/s
(d): Time to Strike the Beach Below the Cliff
We can use the kinematic equation for vertical motion to find the time ttt it takes for the stone to fall to the beach: y(t) = y0 + v0y (t) + (1/2)gt2
Setting y(t)=0, (since it strikes the beach at ground level):
0 = 50 + 0 x t + (1/2) x (-9.8) x t2
Solving for t: 0 = 50 – 4.9t2
Hence, 4.9t2 = 50,
Therefore, t = 3.19 s
(e): Speed and Angle of Impact
The final speed v of the stone when it hits the beach can be found by combining the horizontal and vertical components of the velocity at 3.9 s.
Horizontal component vx :
vx = 18.0 m/s
Vertical component vy :
vy = 9.8 x 3.19 ≈ 31.26 m/s
The magnitude of the final velocity v:
v = √(vx)2 + (vy)2
Thus, v = v = √(18.0)2 + (31.26)2 = 36.06 m/s
The angle of impact θ can be found using the inverse tangent function:
θ = tan-1 (vy/vx) = tan-1 (31.26/18.0) = 60.40
Therefore, the stone strikes the beach with a speed of approximately 36.06 m/s at an angle of 60.40 below the horizontal.