What is Critical Angle and its Formula?

What is a Critical Angle?

Definition: The critical angle is the angle of incidence in the denser medium when the angle of refraction in the less dense medium is ninety degrees (90⁰). The critical angle is a concept in optics that describes the angle of incidence at which light transitions from one medium to another with a higher refractive index, typically from a denser medium (e.g., glass or water) to a less dense one (e.g., air). When the angle of incidence surpasses the critical angle, light no longer refracts into the second medium but instead undergoes total internal reflection, staying within the denser medium.

The formula to calculate the critical angle (θ_c) is given by:

θ_c = sin^-1(n₂ / n₁)

Where:

θ_c is the critical angle.
n₂ is the refractive index of the denser medium.

n₁ is the refractive index of the less dense medium.

This phenomenon has numerous practical applications, such as in fibre optics, where it allows for the transmission of light signals over long distances within the core of optical fibres, preventing signal loss.

At values above the critical angle, the total internal reflection occurs, that is, the refracted ray disappears and a strong reflected ray appears.

A critical angle is the angle of incidence for which the refracted ray emerges tangent to the surface of the angle.

How to Find Critical Angle

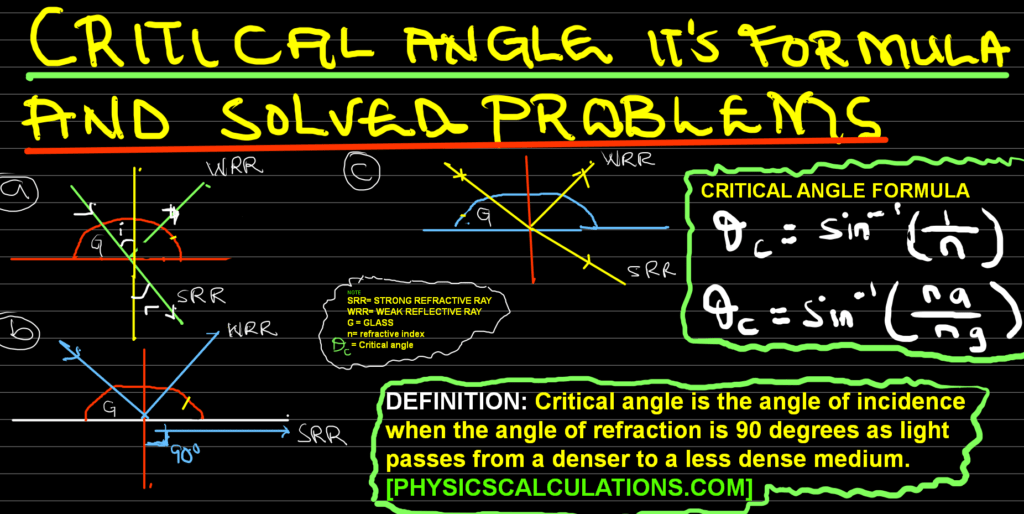
Critical Angle Formula

The critical angle formula is

θ_c = sin^-1 (1 / n) [Where θ_c = critical angle, n = refractive index]

We can also use

θ_c = sin^-1 (n_a / n_g)

Therefore, the critical angle formula that can help us to find critical angle based on the question available to us are: θ_c = sin^-1 (1 / n) or θ_c = sin^-1 (n_a / n_g). Where: θ_c = critical angle, n = refractive index.

Check Questions and Answers on any topic here:

The biggest database of Questions & Answers is available for you! Sign Up Now!

Explanation of Critical Angle

The critical angle is a term in physics and optics to describe the angle of incidence of a ray of light at which it refracts at an angle of 90 degrees to the normal (the line perpendicular to the surface of the medium it is entering).

Let’s assume we allow a ray of light to move from one medium to another. For example, say air to water or from water to glass. This ray of light will change direction because of the change in the speed of light in any of the mediums.

Therefore, we refer to the change in the direction of the ray of light as refraction. The amount of refraction depends on the angle of incidence of the light ray and the refractive index of the two media.

Therefore, to explain the critical angle in the simplest term. We can say that it’s the angle of incidence at which the refracted ray of light is parallel to the boundary between the two media at 90 degrees. In other words, the angle of incidence results in the refracted ray being bent at a 90-degree angle from the normal.

You may also like to read:

what is the critical angle for light traveling from crown glass (n = 1.52) into water (n = 1.33)?

Snell’s Law

We can calculate critical angle by applying Snell’s law. The law states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is equal to the ratio of the refractive indices of the two media.

sin i / sin r = sin θ_c / sin 90⁰ = _gn_a = 1 / _an_g = 1 / n = n_a / n_g

i = Angle of incidence

r = Angle of refraction = 90⁰

θ_c = Critical Angle

_gn_a = Refractive index of the ray of light from glass to air

_an_g = Refractive index of the ray of light from air to glass

n = Refractive index of glass by definition

How to Derive Critical Angle Formula

When the angle of refraction is 90 degrees, the sine of the angle of refraction is equal to one (1). Therefore, the sine of the critical angle is similar to the reciprocal of the refractive index of the two media.

sin r = sin 90⁰ = 1

and sin i = sin θ_c

Thus, sin i / sin r = sin θ_c / sin 90⁰ = sin θ_c / 1 = sin θ_c = _gn_a = 1 / _an_g = 1 / n = n_a / n_g

As stated earlier, the critical angle formula can be written as: θ_c = sin^-1 (1 / n) or θ_c = sin^-1 (n_a / n_g). Where: θ_c = critical angle, n = refractive index.

The critical angle is an important concept in optics. This is because it determines whether a light ray will be refracted or reflected when it encounters a boundary between two media.

If the angle of incidence is greater than the critical angle. The ray of light will be reflected back into the medium from which it came. This phenomenon is called total internal reflection. We use it in various optical devices, such as fiber optic cables, and prism-based cameras.

Relationship Between Refractive Index and Critical Angle

If the refractive angle is 90⁰

By applying Snell’s law, the refractive index for glass – air boundary is: _gn_a = (sin θ_c) / (sin 90⁰)

Now, the refractive index from air to glass is: _an_g = (sin 90⁰) / (sin θ_c)

But sin 90⁰ = 1

Therefore, the refractive index from air to glass is: _an_g = 1 / (sin θ_c)

Total Internal Reflection

When a ray of light passes from an optically denser medium to an optically less dense medium, there exists a weak internal reflection and a strong refraction. But as the angle of incidence increases, the angle of refraction also increases at the same time.

The intensity of the reflected ray gets stronger and that of the refractive ray becomes weaker. When the angle of incidence exceeds the critical angle, there exists no refraction and a total reflection occurs. We refer to this phenomenon in physics as total internal reflection.

The conditions under which total internal reflection occurs are:

Light rays must travel through a denser medium to a less dense medium
The angle of incidence must exceed the critical angle.

Critical Angle Practice Problems

Here are practice problems to help you understand how to calculate critical angle problems:

Problem 1

What is the critical angle for light traveling from water to air? The refractive index of water = 4/3

Data

The refractive index of water, n = 4/3 = 1.33

Unknown

Critical angle = ?

Formula

Critical angle, θ_c = sin^-1 (1 / n)

Solution

We will insert our data into the formula

θ_c = sin^-1 (1 / n) = sin^-1 (1 / 1.33)

We will now have

θ_c = sin^-1 (0.75) = 48.6⁰

Therefore, the critical angle for light traveling from water to air is 48.6 degrees.

Problem 2

A ray of light strikes from a medium with n = 1.67 on a surface of separation with the air with n = 1. Find the value of the critical angle.

Data

The refractive index of air, n_a = 1.67

We also have the refractive index of glass, n_g = 1

Additionally, we have a refractive index of the medium is, n = n_a / n_g = 1 / 1.67

Unknown

Critical angle, θ_c = ?

Formula

The equation for Critical angle, θ_c = sin^-1 (n_a / n_g)

Solution

We will add our data to the formula

Critical angle, θ_c = sin^-1 (n_a / n_g) = sin^-1 (1 / 1.67)

The above expression will give us

θ_c = sin^-1 0.599

And our final result for the critical angle will become

θ_c = 36.8⁰

Problem 3

The refractive index of a medium relative to air is 1.8. Calculate to the nearest degree, the critical angle for the medium.

Data: The information from the question that will help us solve the problem

The refractive index, n = 1.8

Unknown: What we need to find

Critical angle, θ_c = ?

Formula: The equation that will help us solve the problem

Critical angle, θ_c = sin^-1 (1 / n)

Solution

To solve the problem, we will apply the critical angle formula above:

θ_c = sin^-1 (1 / n) = sin^-1 (1 / 1.8) = sin^-1 (0.55) = 33.75⁰

Therefore, we can abbreviate the final answer as 34⁰

Problem 4

The refractive index for a given transparent medium is 1.4. What is the minimum angle for total internal reflection to take place in the medium?

Data: The information from the question

The refractive index for the medium, n = 1.4

Unknown: Unavailable data from the question

Critical angle, θ_c = ?

Formula: The equation that will help us solve the problem

Critical angle, θ_c = sin^-1 (1 / n)

Solution

Critical angle, θ_c = sin^-1 (1 / n) = sin^-1 (1 / 1.4) = sin^-1 (0.714) = 45.6⁰ = 46⁰

Therefore, the critical angle of the medium is 46⁰

Problem 5

If the refractive index of glass is 1.5, what is the critical angle at the air-glass interface?

Data: The information from the question

Refractive index, n = 1.5 = 3 / 2

Unknown: What we need to find

Critical angle, θ_c = ?

Formula: The equation to solve the problem

Critical angle, θ_c = sin^-1 (1 / n)

Solution

Critical angle, θ_c = sin^-1 (1 / n) = sin^-1 (1 / 1.5) = sin^-1 (1 / (3/2))

Therefore, the critical angle, θ_c= sin^-1 (2 / 3) = sin^-1 (0.667) = 41.8⁰ = 42⁰

Problem 6

The refractive indices of glass and water are 1.5 and 1.3 respectively. What will be the critical angle when the angle of refraction in the water medium is 90⁰?

Data:

The refractive index of water, n_w = 1.3

Refractive index of glass, n_g = 1.5

Refractive angle, θ = 90⁰

Unknown:

Critical angle, θ_c = ?

Formula:

θ_c = sin^-1 (n_w sin90⁰)/ n_g

Solution

sin θ_c = (n_w sin90⁰)/ n_g = (1.3 x 1) / 1.5 = 0.866

θ_c = sin^-1 (0.866) = 60⁰

Table for Substances Their Critical Angles and Refractive Indexes

substance	Refractive index (n)	Calculation θ_c = sin^-1 (1 / n)	Critical angle (θ_c)
Vacuum	1.00	θ_c = sin^-1 (1 / 1)	90⁰
Pure Water	1.33	θ_c = sin^-1 (1 / 1.33)	48.75⁰
Carbondioxide	1.0005	θ_c = sin^-1 (1 / 1.0005)	88.19⁰
Ice	1.31	θ_c = sin^-1 (1 / 1.31)	49.76⁰
Ethyl Alcohol	1.36	θ_c = sin^-1 (1 / 1.36)	47.33⁰
Quartz	1.46	θ_c = sin^-1 (1 / 1.46)	43.23⁰
Vegetable oil	1.47	θ_c = sin^-1 (1 / 1.47)	42.86⁰
Olive oil	1.48	θ_c = sin^-1 (1 / 1.48)	42.51⁰
Acrylic	1.49	θ_c = sin^-1 (1 / 1.49)	42.16⁰
Table Salt	1.51	θ_c = sin^-1 (1 / 1.51)	41.47⁰
Glass	1.52	θ_c = sin^-1 (1 / 1.52)	41.14⁰
Sapphire	1.77	θ_c = sin^-1 (1 / 1.77)	34.40⁰
Zircon	1.92	θ_c = sin^-1 (1 / 1.92)	31.39⁰
Cubic zirconia	2.16	θ_c = sin^-1 (1 / 2.16)	27.58⁰
Diamond	2.42	θ_c = sin^-1 (1 / 2.42)	24.41⁰
Gallium phosphide	3.50	θ_c = sin^-1 (1 / 3.50)	16.60⁰

Table For Substances their refractive indexes and critical angles

Sources:

Researchgate

Google Books

American chemical society

Gemology project

Libretext