Question
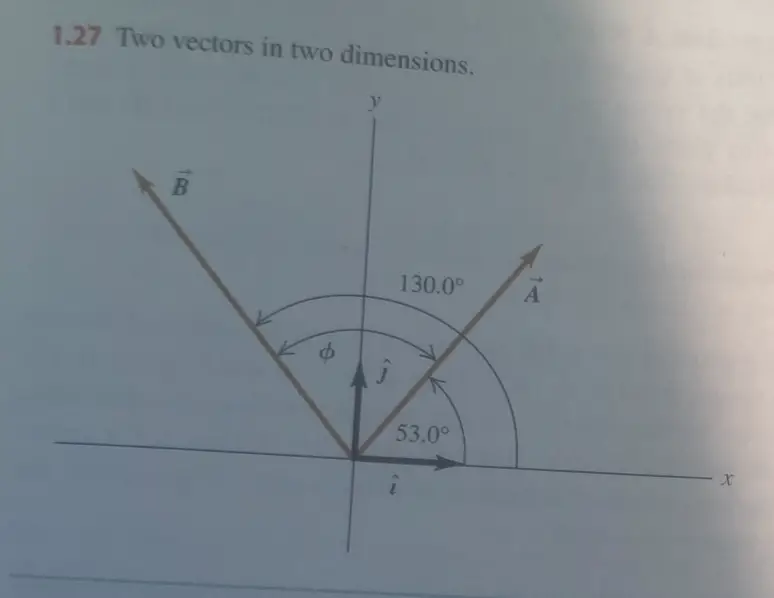
Find the scalar product Ä – B of the two vectors in Fig. 1.27. The magnitudes of the vectors are A = 4.00 and B = 5.00.
Answers
IDENTIFY: We are given the magnitudes and directions of A and B, and we wish to calculate their scalar product.
SET UP: We will calculate the scalar product in two ways: using the magnitudes of the vectors and the angle between them (Eq. 1.18), and using the components of the two vectors (Eq. 1.21).
EXECUTE: With the first approach, the angle between the two vectors is & = 130.0° – 53.0° = 77.0°, so
A • B = ABcos = (4.00) (5.00) cos 77.0° = 4.50
This is positive because the angle between A and B is between 0° and 90°.
To use the second approach, we first need to find the components of the two vectors. Since the angles of Á and B are given with respect to the +x-axis, and these angles are measured in the sense from the +x-axis to the +y-axis, we can use Eqs. (1.6):
Ax, = (4.00) cos 53.0° = 2.407
Ay, = (4.00) sin 53.0° = 3.195
Az, = 0
Bx, = (5.00) cos 130.0° = – 3.214
By, = (5.00) sin 130.0° = 3.830
Bz = 0
The z-components are zero because both vectors lie in the xy-plane. As in Example 1.7, we are keeping one too many significant figures in the components; we’ll round to the correct number at the end. From Eq. (1.21) the scalar product is
A •B = AxBx + AyBy + AzBz= (2.407) (-3.214) + (3.195) (3.830) + (0) (0) = 4.50
EVALUATE: We get the same result for the scalar product with both methods, as we should.