Question
The motorcycle is traveling at a constant speed of 76km/h. Determine the magnitude of its acceleration when it is at point A.
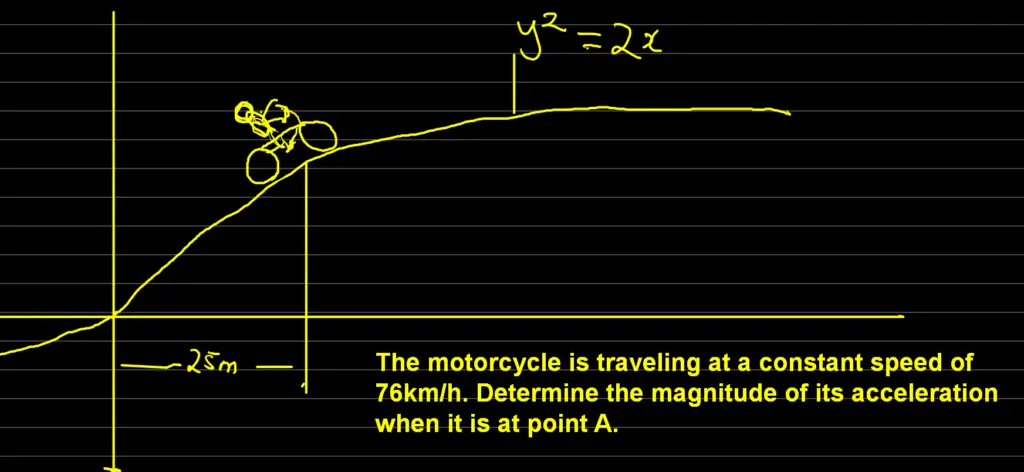
Answer
The magnitude of its acceleration when it is at point A is 1.223 m/s2.
Explanation
Data: The information from the question
Constant speed, v = 76 km/h = (76 x 1000) / (60 x 60) = 76000 / 3600 = 21.1 m/s
The tangential acceleration, at = dv/dt = 0
x = 25 m
We also have y2 = 2x. Thus, we can take the square root of both sides to end up with y = √2x
But since x = 25, we can then say that y = √2x = √2 x 25 = √50. Therefore, y = √50.
Unknown: The information we need to find
The normal acceleration, an = ?
Formula: The equation that will help us to solve the problem
First step: We will apply the first and second derivatives of 2x
Second Step: We will use the product rule
Third step: We will now employ the equation for the radius of the curvature ρ = [1 + (dy/dx)2]3/2 / (d2y/dx2)
Fourth Step: We will finally apply the formula an = v2 / ρ
Solution
First step:
y2 = 2x
After differentiating the above equation, we will now have
2y (dy/dx) = 2
We can now divide both sides by 2y to obtain
(dy/dx) = 1/y
Second step:
We will now use the product rule
2y (d2y/dx2) + 2 (dy/dx)2 = 0
After collecting like terms and dividing both sides by 2y, we will get:
(d2y/dx2) = – (1/y)(dy/dx)2
We can now substitute our data into the above equation
(d2y/dx2) = – (1/√50)(dy/dx)2
But dy/dx = 1/√50
Therefore,
(d2y/dx2) = – (1/√50)(1/√50)2
We will now have
(d2y/dx2) = (1/(50√50))
(d2y/dx2) = (1/353.6) = 0.00283 = 2.83 x 10-3
Remember that dy/dx 1/√50 = 0.141
Third step:
We will now use the formula ρ = [1 + (dy/dx)2]3/2 / (d2y/dx2) to find the radius of the curvature (ρ).
ρ = [1 + (dy/dx)2]3/2 / (d2y/dx2) = [1 + (0.141)2]3/2 / (2.83 x 10-3) = 363.95 m
Fourth step:
The final step is to use the formula an = v / ρ to find the magnitude of the acceleration. Therefore
an = v2 / ρ = (21.1 m/s)2 / (363.95 m) = 445.21 m2/s2 / 363.95 m = 1.223 m/s2
Therefore, the magnitude of the acceleration is 1.223 meters per second square (m/s2)
You may also like to read: